我们知道，理想液体运动时，由于没有黏性作用 （μ=0），所以液体质点间没有切应力τ存在，只有动水压强p。但是，当黏性液体运动时，液体质点间除去法向存在假想的平均动水压强p以外，还存在着由于液体黏性所引起的附加正应力和附加切应力。对于图10.7.1所示的边长分别为d x，d y、d z的微元六面体，仿照材料力学，令微元体在三个坐标平面上的应力分别为σx、τxy、τxz，σy、τyx、τyz，σz、τzx、τzy。其中σx、σy、σz是微元体在三个坐标平面上的正应力。它们可以用假想的平均动水压强和由于液体黏性所引起的附加正应力表示成为：

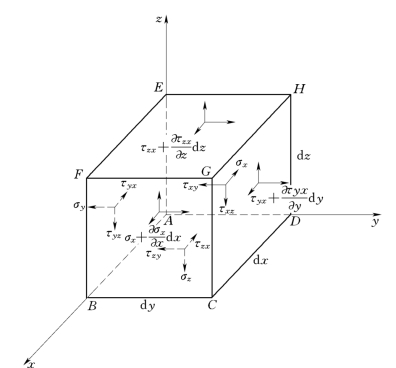
图10.7.1

平均动水压强p前的负号是由于它与受力作用面的外法向方法相反而加的。其余六个是切应力。切应力中的第一个脚标表示受力面的法线方向，第二个脚标表示应力的方向。又根据材料力学中的切应力互等定理可知：

在材料力学中应力与应变速度 （单位时间内的变形）成比例，即正应力与伸缩变形速度有关，切应力与剪切变形速度有关，这一点与材料力学不同。根据斯托克斯定律 （广义牛顿内摩擦定律），对于不可压缩液体，液体中的附加正应力和切应力与变形速度具有下述关系：

根据式（10.7.3）和式（10.7.1）可写成：

即黏性液体中的动水压强p，是通过给定点处三个相互垂直的微元面积上的法向应力的算术平均值来定义的。这样，动水压强p只是空间坐标和时间的函数，而与受力作用面的方位无关。

下面对图10.7.1所示的微元控制体应用动量方程式（3.3.10）建立运动微分方程：

以x方向为例，单位质量力为X，表面应力为σx、τyx、τzx。代入作用力后x方向的动量方程为：

对式（10.7.7）左端各面积分项应用高斯定理变成体积分，并利用式（10.7.4）和式（10.7.5）。

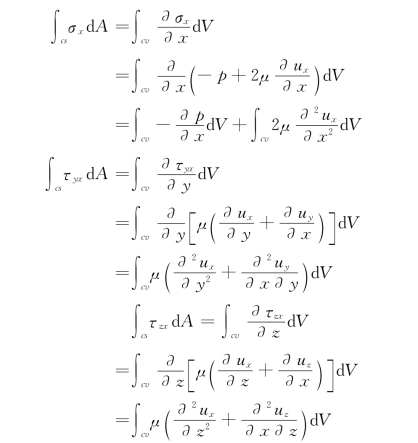
式 （10.7.7）右端项参见式（10.4.7）的推导，得：

将上面各项代入式（10.7.7）并加以整理，得：

注意到上式左端第三项为0，然后去掉两端的积分号并除以ρ，又ν=μ/ρ，再引入微分算子

最后得：

式 （10.7.9）的向量形式为：

式 （10.7.9）和式（10.7.10）是不可压缩黏性液体的运动方程，也称为纳维—斯托克斯（Navier Stokes）方程，以后就简称为N S方程。它是二阶非线性的偏微分方程组，只有在忽略非线性项或者非线性项线性化以后才能同连续方程联立求解。(www.daowen.com)

为了以后引用方便，下面给出柱坐标中的N S方程和连续性方程。

在柱坐标中：

例10.7.1 如图10.7.2所示，黏性液体在较长的水平圆管中作恒定有压层流运动。已知圆管半径为r0。试应用N S方程推求圆管层流过水断面上的流速分布式。

图10.7.2

解：

为推导方便，我们采用如图10.7.2所示的柱坐标系统，但z轴用x轴代替。根据题意，①由于是恒定流，所以∂（ ）/∂t=0；②由于质量力只有重力，同黏性项相比可以忽略，即Ωr=Ωθ=Ωx=0；③由于是轴对称流动，所以vr=vθ=0。又令vz=u=u （r）。将上述结果代入柱坐标的N S方程式（10.7.11）和连续方程 （10.7.12）后，得下面简化了的方程组：

由式（10.7.13）、式 （10.7.14）可知：

即压强在断面上没有变化，只在流动方向上变化。

由于式（10.7.18）左端只是r的函数，右端只是x的函数，为了使左右两端相等，它们只能等于某个常数，即

现将式（10.7.18）两端同时除以r，得：

再将C1、C2代回式（10.7.21），得圆管中层流流动时的流速分布公式为：

令式中r=0，则得管中的最大速度为：

将式（10.7.23）代入式（10.7.22），得：

可见圆管层流中流速按抛物线分布。

有了流速分布以后就不难求出圆管中的流量Q和断面平均流速um。

结论：在圆管恒定层流中，当不计重力作用时，①压强在横断面上均匀分布，沿管轴方向按直线规律减小；②轴向流速在横断面上按抛物线规律分布，如图10.7.2所示。