图10.6.3所示为一流网，其中φ和ψ值按上节讲述的法则标定，即流速势函数φ的增值方向与流速u的方向相同；流函数ψ值的增值方向与流速u逆时针旋转90°的方向相同，此法则称为儒可夫斯基法则。这样，只要知道流速u的方向就可以确定出φ和ψ的增值方向。

流网具有如下两个性质。

1.流线与等势线正交

在等势线上，下面的微分方程成立：

在流线上，下面的微分方程成立：

从而得等势线和流线的斜率分别为：

图10.6.3

现在，作等势线和流线斜率的乘积，并利用柯西—黎曼条件，得：

由解析几何可知，等势线与流线正交。

2.当dφ=dψ时，流网的网眼将成曲边正方形

如图10.6.4所示，在平面势流场中任取一点p，过p点画出一条等势线φ和一条流线ψ，并画出它们相邻的等势线φ+dφ和流线ψ+dψ，形成一个网眼。令两条相邻等势线之间的距离为d s，两条相邻流线之间的距离为d n。

由式（10.6.4）和式（10.6.11）得：

(www.daowen.com)

故

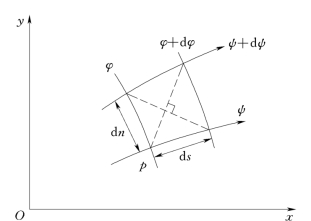
图10.6.4

即证明了当dφ=dψ时流网的网眼是曲边正方形。需要说明的是：这里所说的正方形与几何上的正方形并不完全相同，只要网眼的对角线互相垂直且相等就可以认为网眼是曲边正方形。

实际上，在平面势流的流场中，不可能绘制无限多的等势线和流线，因此式（10.6.19）应改写成差分形式，即

又由此式和式（10.6.11）得：

即每两条流线间通过的流量相等。这样，应用起来就非常方便。

由式（10.6.21）可求得两条流线间任意两个网眼上的流速之比，即

当已知某个网眼的Δn1和速度u1，并由流网图中量得其他网眼的Δn，则由式（10.6.22）就可以求得其他网眼的流速u，从而也就解决了平面势流场中的流速分布问题。

如果平面势流中某点（网眼中点）的位置z1、压强p1和流速u1已知，则根据欧拉能量方程就可以求得流场中任意一点的压强为：

这样平面势流中的压强分布也就求出来了。

从上述可知：如果能画出一个较为准确的流网，就相当于解一个欧拉运动微分方程组（包括连续方程），或者解一个拉普拉斯方程。由于在一般条件下用解析法解偏微分方程在数学上存在一定困难，因此工程中许多解析法难以解决的问题常可借助流网法解决。