不可压缩液体平面运动的连续方程为：

又平面流动中的流线方程为：

由高等数学可知：式 （10.6.7）是使式（10.6.8）的左端成为某个函数全微分的充分必要条件。假设此函数为ψ（x，y），则

又

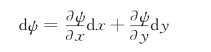
对比上面两式得：

函数ψ称为流函数。

因为流函数存在的条件是要求流动满足不可压缩液体的连续性方程，而满足连续性方程这是任何流动都必须遵循的，所以说任何平面流动中一定存在着一个流函数ψ，这个ψ就描绘一种由式（10.6.9）所表示的平面流动。因此只要找到平面流动的流函数ψ就可以确定该平面流动的速度场u（ux，uy）。

流函数具有下面的性质。

（1）流函数ψ对任意方向m 的偏导数，等于流速u在m 方向顺时针旋转90°后m′方

向上的流速分量um′，如图10.6.1所示。因为

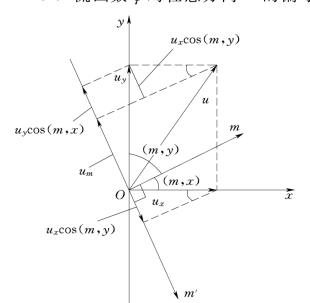
图10.6.1

（2）流函数为常数代表一条流线。

将式（10.6.9）代入上式，得：

(www.daowen.com)

当ψ为常数时，dψ=0，所以上式成为流线方程。

即ψ等于常数时代表一条流线，不同的常数代表不同的流线流，流函数就是由此而得名的。

（3）流函数沿流线s方向逆时针旋转90°后的n方向增大。由流函数性质（1）得：

又由流函数性质（2）得∂ψ/∂s=0，所以上式就可以写为：

因为式（10.6.11）中u＞0，所以流函数ψ增值方向与n值的方向相同。

（4）通过两条流线间的单宽流量q等于这两条流线的流函数值之差ψ2-ψ1。如图10.6.2所示，设在平面流场中有两条流线s1与s2，它们的流函数值分别为ψ1 和ψ2。因为是平面流动，在z轴方向可取单位长度1，所以两条流线间所通过的流量称为单宽流量，记为q。在两条流线间取微元过水断面面积d n×1，设其上的流速为u，则通过的流量为：

由式（10.6.11）知dψ=u d n，代入上式后沿过水断面1-2积分，得：

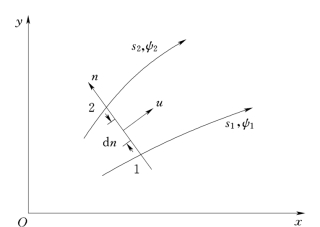
图10.6.2

（5）平面无涡运动的流函数也是调和函数。流函数的前面四个性质与流动有涡无涡没有关系，但是，当液体作无涡运动时又具有下面性质。对于x Oy平面上的无涡运动有：

将式（10.6.9）中的ux= ∂ψ/∂y，uy=-∂ψ/∂x代入上式，得：

或

即在平面势流中流函数ψ也满足拉普拉斯方程，也是调和函数。