10.3节建立的连续性方程只反映了液体运动的运动条件，即液体质点速度之间的关系，它没有说明液体运动的动力条件，即作用力与质点速度之间的关系，而本节要建立作用在理想液体上的力与质点速度之间的关系，即建立欧拉运动微分方程。

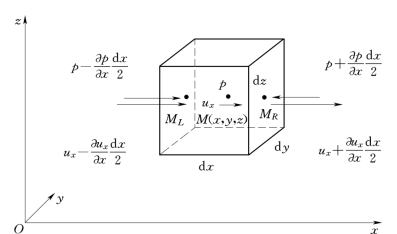
图10.4.1

对于x方向上式变为：

为了积分式（10.4.1）需要应用数学上将面积分与体积分相互转化的高斯定理。该定理表达式为：

它说明向量A在闭曲面S上的面积分等于向量A 的散度▽·A在闭曲面S所围的体积V上的体积分。

作用在控制体上x方向上的质量力为：

考虑到控制体体积上的表面力不随时间变化，式 （10.4.1）右端第一项的偏微分符号可移到积分号内，即

(www.daowen.com)

式 （10.4.1）右端第二项用高斯定理变为：

将式（10.4.3）～式 （10.4.6）代入式（10.4.1），并去掉两端的积分符号得：

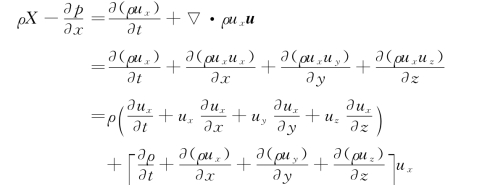
根据连续方程（10.3.3），上式右端最后一项中括号内等于0。然后将上式两端同除以ρ，最后得x方向的运动微分方程为：

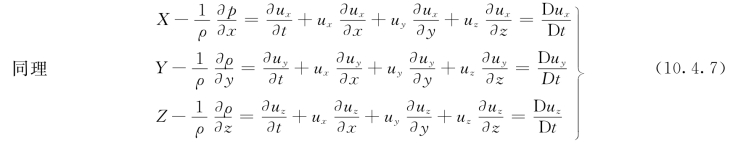
式 （10.4.7）就是理想液体的运动微分方程，也称为欧拉运动微分方程，它是由欧拉在1775年首先导出的。

式 （10.4.7）中的x、y、z、t是自变量，p、ux、uy、uz是x、y、z、t的未知函数。X、Y、Z也是x、y、z的函数，一般是已知的。三个运动方程有四个未知数，为了求解还需加入一个连续方程，对于不可压缩液体为：这样方程的数目与未知数的数目相等，由式（10.3.6）及式（10.4.7）在一定的初始条件下可以求解p、ux、uy、uz。

物体表面法线方向上的速度un等于0就是一种边界条件，即

初始条件和边界条件对于不同问题有不同的形式，这里不作详细论述，可参考有关著作。