在第3章中应用控制体概念已经推求出一元流的连续性方程式（3.4.6）。下面将应用控制体概念根据质量守恒定律，导出液体三元运动连续方程。

在如图10.3.1所示的直角坐标系中，取出边长分别为d x、d y、d z的微元直角六面体作为控制体。设六面体中点M（x，y，z）处的速度为u（ux，uy，uz），密度为ρ。

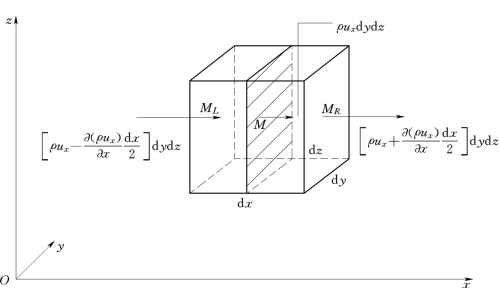
图10.3.1

现以x方向为例。u是中心点M的速度，ux是u在x方向的分速度，ρux是单位时间内通过单位面积的质量，称为M点处的质量密度。将ρux在M点的邻域按泰勒级数展开，并略去二阶以上的高阶小量，则得六面体左右侧面上中心点ML和MR处的质量密度分别为：

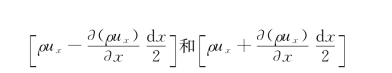
假设质量密度在ML和MR所在的平面上均匀分布，则单位时间内流入流出这两个平面的质量分别为：

单位时间内x方向上流出与流入控制体的液体的质量差则为：

同理可得单位时间内在y、z方向上流出与流入控制体的液体质量差分别为：

单位时间内流出与流入控制体的液体总的质量差为：

根据连续方程（3.4.1），式 （10.3.1）与式（10.3.2）之和应等于零，得：

或写成(www.daowen.com)

式 （10.3.3）～式 （10.3.5）就是液体三元运动的连续方程。

对于不可压缩液体，不管是恒定流还是非恒定流，∂ρ/∂t=0，所以连续性方程为：

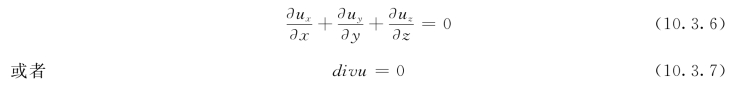
div u称为速度u的散度。它是液体的体积变化率。对于不可压缩液体，且内部没有奇点（源或者汇），速度u的散度一定为0。此条件约束着微团的变形，若液体微团在一个方向上伸长，则在另外两个方向上至少有一个方向上是缩短的。若速度u的散度不为0，说明流场内一定有奇点（源或者汇）存在。

例10.3.1 已知空间流动的速度分量分别为ux=2x+1，uy=4y+2，uz=6z+3试求：通过图10.3.2所示的中心在坐标原点半轴长分别为a=1.0m，b=0.8m，c=0.6m的椭球表面的流量Q。

解：

通过整个球表面的流量可以用下面的面积分计算，即

根据面积分与体积分之间的关系有：

图10.3.2

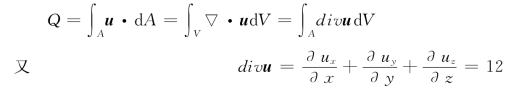
故得：