在液体流动时,当液体微团存在着绕自身轴的旋转运动时,即ω≠0时的流动称为有涡流。和10.1节对比,如果说求解无涡流(即势流)的关键在于求出全流场流速势函数φ的分布φ(x,y,z;t),那么在有涡流中关键则是求出全流场各点的旋转角速度矢量ω(x,y,z;t),所以说有涡流可以用旋转角速度或旋涡矢量ω表示。如同速度场一样存在着涡场,同时在涡场中也有涡线、涡管、元涡及涡量等概念。
1.涡线、涡管、元涡及涡量
涡线是一条瞬时曲线,在同一瞬时,在这条曲线上所有空间点处的旋涡向量与该曲线相切。设旋涡向量ω(ωx,ωy,ωz),则涡线微分方程为:
![]()
对于非恒定流,上式中的t为参数,恒定流时则不出现t。
在涡场中通过某一闭曲线上各点的涡线所形成的管称为涡管。
横断面面积很小的涡管内的流体称为元流或者涡束。
设元涡的横断面面积为d A,液体微团的平均旋转角矢量或旋涡矢量ω(ωx,ωy,ωz),则我们将元流的横截面面积d A与2倍旋涡矢量ω的点积定义为元涡的涡量或涡管强度,对于整个涡管横断面上的涡量或涡管强度记为J,则
![]()
涡线、涡管、元涡及涡量如图10.2.2所示。
2.速度环量
在流场中取一闭曲线s,设线元向量为d s=d x i+dy j+d z k,其上速度向量为u=uxi+uyj+uzk,u在d s方向的分量为ut=|u|cosθ,如图10.2.3所示。我们将ut与d s的乘积沿闭曲线s积分定义为速度环量,即
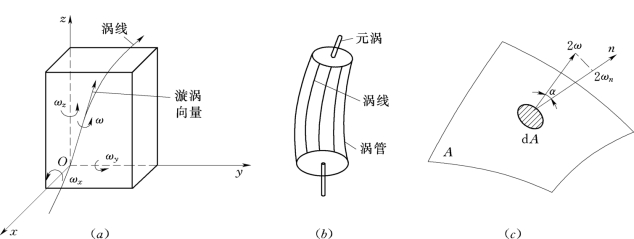
图10.2.2
![]()
式中 θ——d s与u的夹角。
注意:速度环量是标量;速度方向与积分路径方向一致时Γ为正。一般取逆时针方向积分路径为正,即逆时针方向的速度环量为正。速度环量Γ具有瞬时性。
当流动为无涡流,即势流时:
![]()
代入式(10.2.8),得:
![]()
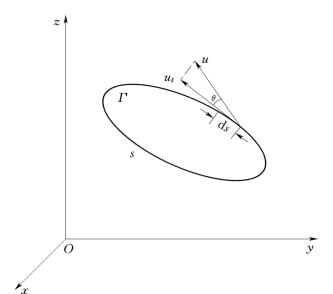
图10.2.3
当流速势函数φ为单值时,上面的积分为零,则得Γ为零。反之,Γ值不为零时一定是有涡流,这可由下面的斯托克斯定理证明。
3.斯托克斯定理
沿任意闭曲线s的速度环量Γ,等于以此闭曲线为边界的面积A上的涡量J,即
![]()
证明:(https://www.daowen.com)
取如图10.2.4所示的微小矩形边界,各角点的速度如图中所注,现计算速度环量dΓz。
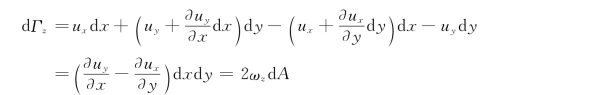
同理,有
![]()
![]()
即微元环量等于微元面积上的涡量,这就是对微元面积而言的斯托克斯定理。对于有限面积A也有同样的结论。如图10.2.5所示,将A平面分成许多矩形和三角形,除面积A周边的速度环量外,内边界的速度环量在相加时都会抵消掉。对于曲面也可以依此类推,最后得:
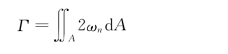
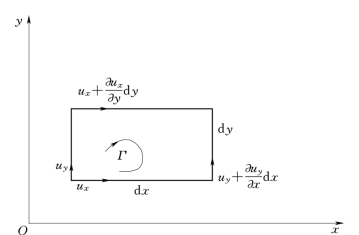
图10.2.4
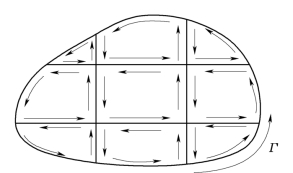
图10.2.5
斯托克斯定理将速度环量与涡量联系起来了。这样,可以通过分析速度环量来研究有涡流。其优点主要有以下两方面。
(1)根据速度环量可以较容易地推求涡量和液体微团的旋转角速度。因为速度环量是线积分,被积函数是速度本身,而涡量是面积分,被积函数是速度的偏导数,当然计算线积分要比计算面积分容易。
(2)液体微团的速度可以测量,但是,涡量和液体微团的旋转角速度不能直接测量。只有当液体微团的旋转角速度为常数时,通过计算涡量求速度环量才更显简便,见例10.2.1。
例10.2.1 已知某平面流动的速度场为![]() 其中a为常数。试求:(1)涡线方程式。
其中a为常数。试求:(1)涡线方程式。
(2)沿闭曲线x 2+y 2=b2的速度环量。
解:
(1)涡线方程式
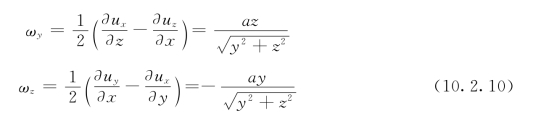
涡线方程式为:


(2)速度环量
在xOy平面上z=0,根据式(10.2.10)涡分量:
![]()
由于ωz=常数,我们应用斯托克斯定理,通过计算涡量来求速度环量,即
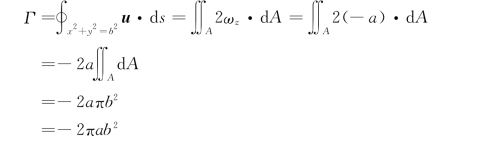
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






