若液体流动时每个液体微团不存在绕自身轴的旋转运动，即ω（ωx，ωy，ωz）=0，则称此流动为无涡流，也称为无旋流；若液体流动时每个微团都存在着绕自身轴的旋转运动，则称此流动为有涡流，也称有旋流。这是两种本质不同的流动。其中应该特别注意的是：涡是指液体微团绕自身轴旋转的运动，不要将涡与液体质点运动的轨迹相混淆。图10.2.1 （a）中的流动是无涡流，图10.2.1 （b）、（c）中的流动是有涡流。

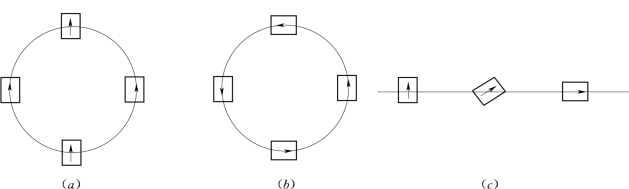
图10.2.1

由无涡流的定义可得：

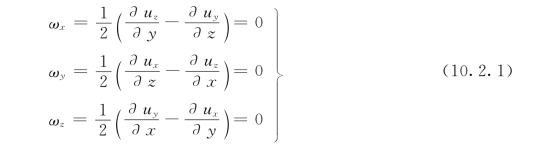
或者

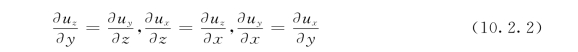(www.daowen.com)

有高等数学可知，式 （10.2.2）是uxd x+uyd y+uzd z为某一函数φ（x，y，z；t）的全微分的充分必要条件，其中t为参变量。于是：

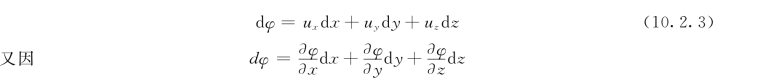
对比上面两式可知：无涡流时必然存在着函数φ（x，y，z；t），它与流速之间存在着下面的关系：

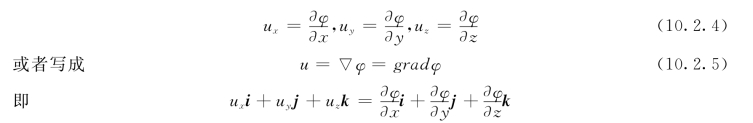
仿照引力场中力势函数的概念，称φ（x，y，z；t）为流速势函数，▽φ和gradφ称为流速势函数φ的梯度。由于无涡流中存在着流速势函数，因此也称无涡流为势流。但是，流速势函数不具有势能的意义。

由式（10.2.4）可知：在指定的瞬时t，流速势函数为某一方向的偏导数等于速度向量u在该方向上的投影。所以求解势流问题就归结为求流速势函数φ。