速度分解定理是用液体微团基本运动形式表示液体微团内任意相邻两点之间速度关系的定理。

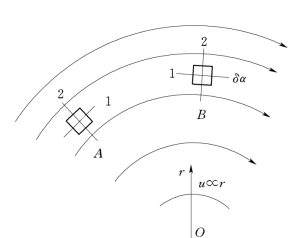
图10.1.3

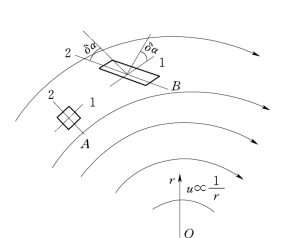
图10.1.4

设在时刻t，某液体微团内点p（x，y，z）的速度为u（ux，uy，uz），在同一时刻，在此液体微团上点p邻近点Q（x+d x，y+d y，z+d z）的速度为u+d u（d ux，d uy，d uz）。两点间的速度差为d u，用泰勒级数展开后，并略去级数中的二阶以上各项，则两点间的速度差d u（d ux，d uy，d uz）可近似表示为：

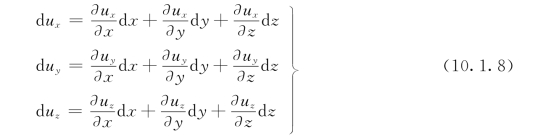
为了便于分析各项的物理意义，以式 （10.1.8）中第1个表达式为例，将右端第2、第3项写成为：

在式（10.1.9）中令：(www.daowen.com)

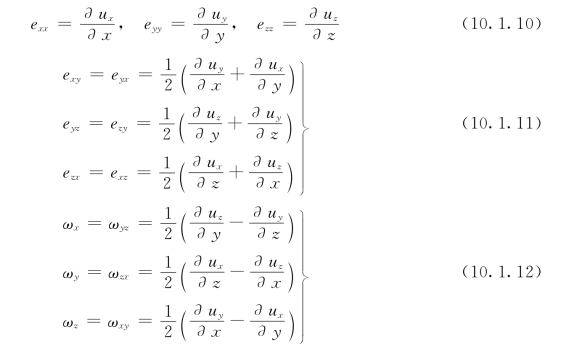
将式（10.1.10）～式 （10.1.12）代入式（10.1.9），并考虑到点p的速度为up=u，点Q的速度为uQ=u+d u，最后得：

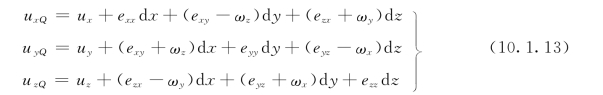
式（10.1.13）就是速度分解定理的具体表达式，也称为亥姆霍兹（H.von.Helmholtz）定理。它说明液体微团上任意一点p （x，y，z）邻近点Q（x+d x，y+d y，z+d z）的速度可分解为三部分：①与p点相同的平移速度；②变形在Q点引起的速度；③绕p点旋转在Q 点引起的速度。由于可以将变形运动从一般运动中分解出来，从而有可能将液体的运动分为无涡（旋）流和有涡（旋）流，从而有可能对它们分别进行研究。因此速度分解定理在水力学中具有重要意义。

由图10.1.5所示，当液体微团由位置A运动到位置B 时，形状由正方形变为平行四边形，各边的长度没有改变。但是，直线1和2间夹角发生了变化，即有剪切变形。同时直线2发生了逆时针方向的旋转，即液体微团有旋转运动。

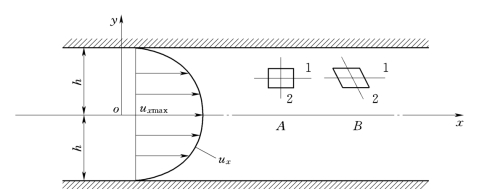
图10.1.5