首先应该明确液体质点与液体微团的区别。液体质点是可以忽略线性尺寸效应 （伸缩、变形和旋转）的液体最小单元，而液体微团是液体质点组成的具有线性尺寸效应的微小液体团。

为了将液体运动加以分类和建立应力应变之间的关系，有必要研究液体微团的运动形式。根据理论力学，刚体有两种运动形式：平移和旋转。而液体运动则不同，由于液体微团在流场中各点速度不同，但又要保证液体本身的连续性，因此液体微团除有平移和旋转运动外，还有变形运动。下面将分析液体微团运动的三种形式。

为了更清楚地说明问题，我们只研究如图10.1.1所示的平面运动中的液体微团。设在t时刻液体微团为矩形ABCD，经过d t时段后移动到新的位置并变形为A′B′C′D′。又设t时刻A 点的时速为ux、uy，根据泰勒级数展开，得B、C点的速度分别为：

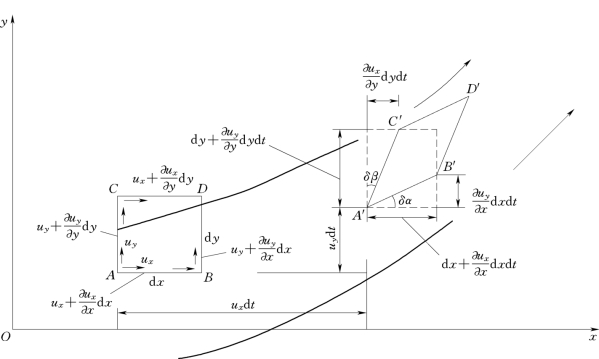
图10.1.1

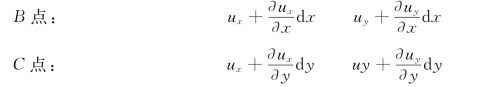
1.平移运动

各点的速度中均包含有ux、uy由图10.1.1可见，ux、uy是平移速度。

2.变形运动

（2）剪切变形。我们将平面上角变形速度的一半定义为液体微团的剪切变形速度，记为eij（i，j=x，y，z，但i≠j）。由图10.1.1可知：A点角速度为：

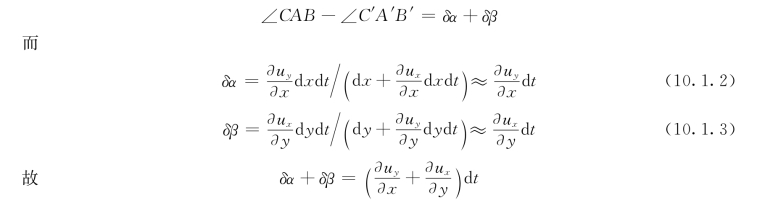(www.daowen.com)

根据液体微团剪切变形速度的定义得：

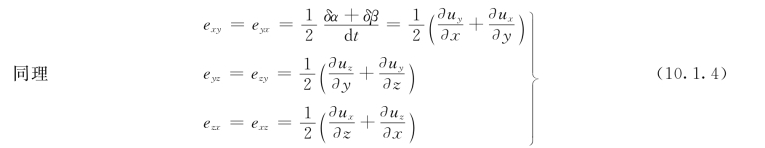
3.旋转运动

式中 rot u——速度u的旋度。

图10.1.2所示为一理想液体在收缩管中的流动。当液体微团由A移动到B 点时，只有伸缩变形，而没有剪切变形和旋转运动。因为微团上的两条直线1与2之间的夹角及其方向没有变化。

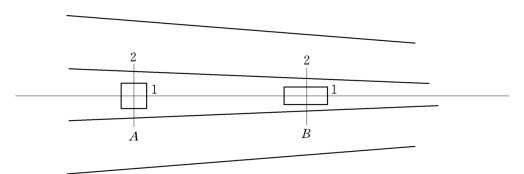
图10.1.2

图10.1.3可视为旋转水桶中的水流运动。设这时液体微团的速度u与旋转半径r成正比。若直线1沿流线顺时针方向旋转某一个角度δα，则由于直线2的外端速度大于内端速度，所以直线2也顺时针旋转相同的角度δα。又液体微团的旋转角速度是两条直线旋转角度的平均值，所以该微团有旋转运动。但是它没有剪切变形，因为直线1、2始终保持垂直，即夹角没有变化。

图10.1.4可视为水轮机导轮中的水流运动。设这时液体微团的流速u与半径r成反比。若微团上的直线1沿流线顺时针方向旋转一个角度δα，则由于直线2的外端速度小于内端速度，所以直线2逆时针方向旋转相同的角度δα。根据液体微团旋转角速度的定义，最后液体微团的旋转角速度为0，即无旋转运动。但是由于直线1、2间的夹角发生变化，因此有剪切变形。