当建筑物下游产生如图9.3.2所示的远驱式水跃时，也可以采用修建消能墙，使墙前水位壅高，以期在池内能发生稍有淹没的水跃。其水流现象与降低护坦的消能池相比，主要区别在于池出口不是淹没宽顶堰流而是淹没折线型实用堰流。水力计算的主要任务是确定墙高C及池长lB。

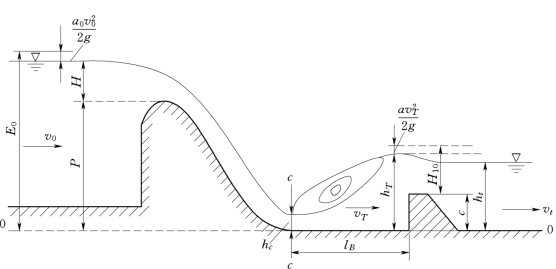
图9.3.2

假设池中产生稍许淹没的水跃。由图中的几何关系可以得出：

式中 h″c——临界水跃的跃后水深；

H10——折线型实用堰的堰上总水头，用下面的公式计算：

式中 m——折线型实用堰的流量系数，一般取m=0.42。

将H0代入式（9.3.8）后，得出：

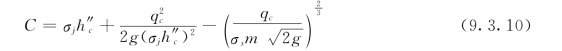
式 （9.3.10）是计算消能墙高度的基本公式。式中σs是消能墙的淹没系数，见表9.3.1。

表9.3.1

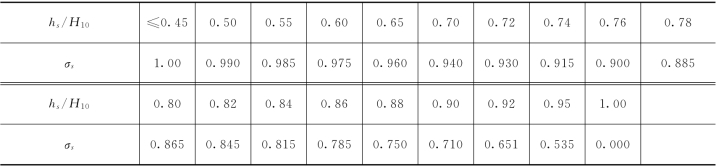
根据表9.3.1可拟合出下面的公式：

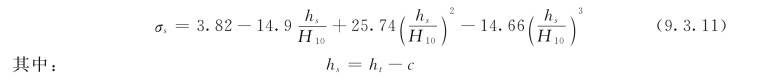(www.daowen.com)

式中 hs——消能墙上的下游水深；

H10——消能墙上的总水头。

从表9.3.1可以看出：

（1）当 （ht-c）/H10≤0.45时，消能墙为自由溢流，这时淹没系数σs=1。

（2）当（ht-c）/H10＞0.45时，消能墙为淹没出流，这时淹没溪水σs＜1。

消能墙的水力计算步骤：

（1）按式（9.2.1）和式（9.2.4）计算hc和h″c。

（2）假设消能墙为自由出流，即σs=1，由式（9.3.10）求出墙高c。

（3）检查消能墙是否为自由溢流。先由式 （9.3.9）计算出 H10，再计算（ht-c）/H10，然后分两种情况：

1）如果（ht-c）/H10＞0.45，则消能墙为淹没溢流，上述假设错误，应该降低墙高，以增加墙上水头，使消能墙通过要求的流量qc。这时也只能采取试算法求墙高，重设墙高c′＜c，由下式计算墙上的水头：

再计算（ht-c′）/H′10，当此值大于0.45时，由表9.3.1或式 （9.3.11）求σ′s。最后计算墙高为c′的淹没溢流时通过的单宽流量：

如果q=qc，则说明假设的墙高即为所求。否则重新假设墙高。当消能墙为淹没溢流时，无需再检查墙后的水流衔接形式，肯定是淹没水跃衔接。这时只设一级消能墙即可。

2）如果（ht-c）/H10≤0.45，则消能墙为自由溢流，墙高计算正确，但是，这时需要检查消能墙下游的水流衔接形式。若为淹没式水跃衔接，则无需建造第二道消能墙；若为远驱式水跃衔接，还需修建第二道消能墙，如果第二道消能墙仍为自由溢流时，还需检查其后的水跃衔接形式，直到消能墙为淹没溢流或其后为淹没水跃衔接为止。一般消能池不宜超过3级。再检查消能墙后的水流衔接形式时，可取消能墙的流速系数φ=0.9。