在很多情况下需要计算天然河道的水面曲线。例如当在河道上修建壅水建筑物，如闸、坝等时，这时壅水建筑物将抬高河道中的水位，为了估计淹没损失，需要计算水面曲线。当整治河道，如疏浚、裁弯取直、分流等时，这时也将改变河流的水力条件，为了正确地确定堤防的高程和断面尺寸，也需要计算水面曲线。本节只介绍恒定流情况下天然河道的水面曲线计算的基本原理。

天然河道有如下特点：①河道在平面图上曲曲弯弯，曲直相间；②河道的过水断面形状、尺寸、底坡及粗糙系数沿流程变化；③在同一断面内水面宽度及粗糙系数随高程不同而变化。因此，在作河道的水面曲线计算之前，根据河道的平面图和纵剖面图，需要将整个河道分成若干个平面尺寸和底坡大致相同的计算流段，使每个计算流段的水力要素平均值能够近似地反映实际水流的情况。

研究天然河道的水面曲线仍可用伯努利能量方程。但是，由于河道的底坡沿程变化，因此水深也沿程变化，故应用以水位表示的能量方程式更方便些。对如图7.7.1所示的流量为Q、相距为Δs的断面1-1和断面2-2写伯努利方程，得：

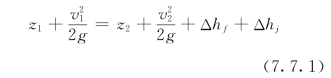
其中沿程水头损失可以用微段的平均水力坡度表示成：

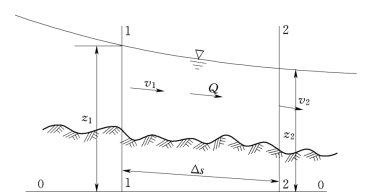
图7.7.1

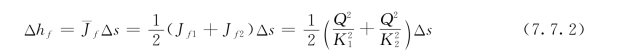
局部水头损失可以用流速水头变化表示成：

式中 ζ——河道的局部水头损失系数，对于逐渐扩散段为-0.55～-0.33，对于急剧扩散段为-1.0～-0.5，对于收缩段为0。

将式（7.7.2）、式 （7.7.3）代入式（7.7.1），得：

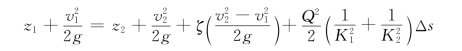
将上式中脚标为1的各项移至等号的左端，脚标为2的各项留在等号的右端，并注意到v=Q/A，则得：

式 （7.7.4）就是天然河道水面曲线计算的基本公式。

当忽略局部水头损失和两断面的流速水头差时，式 （7.7.4）可以简化为：

(www.daowen.com)

计算天然河道水面曲线的式 （7.7.4）或式 （7.7.5）和计算人工渠道水面曲线的式（7.6.4）在本质上没有区别。不同的是式（7.7.4）或式（7.7.5）不用水深h而用水面高程z作参数，直接计算水位z随距离s的变化。因此式中的流量模数K=C A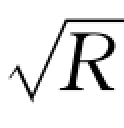不用水深h去求出，而应由R=A/X直接求出，为此必须对河道各计算断面测量出面积A和湿周X与水面高程z的关系曲线，即A=A（z）和X=X（z）。当用水面宽度B代替湿周X时则B =B（Z）。

式 （7.7.4）和式（7.7.5）的左端是水位z1的函数，右端是水位z2的函数。在天然河道的水面曲线计算中，一般是已知计算流段下游断面的水位z2，故上面两式的右端是某个已知量。从而可知：天然河道水面曲线的基本解法是试算法，即假设一系列计算流段上游断面的水位z1，从中找出满足上面两式的z1作为解。然后将此z1作为其上游计算流段的z2，重复上述步骤就可以求得整个河道的水位与距离的关系曲线z=f（s）。

对于式 （7.7.5），除了试算法外，还有各种不同的图解法，如拉哈曼诺夫（A.H.Pax Ma HoB）方法，艾斯考弗（F.F.Esc offer）方法等。这里就不予介绍了，需要时可参考有关书籍。

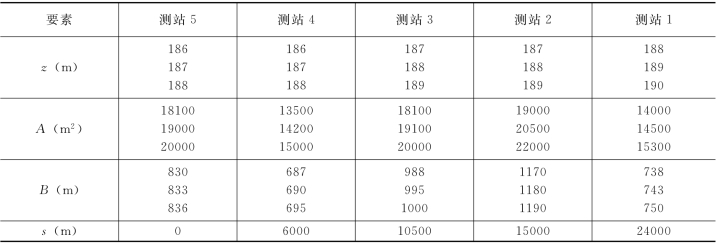
例7.7.1 如图7.7.2所示为某河道的纵断面图，今在断面5-5处修建高坝蓄水后，流量Q=26500m3/s时，断面5-5处的水位z5=186.65m河道的粗糙系数n=0.04，各断面间距离Δs和各断面的水位z与过水断面面积A 和水面宽度B 之间的关系见表7.7.1。试求用试算法计算断面4-4的水位z4。

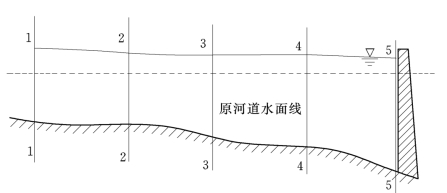
图7.7.2

表7.7.1

解：

为了试算用，首先需要给出5-5断面和4-4断面的水位z与过水断面面积A 和水面宽度B的关系曲线，如图7.7.3所示。

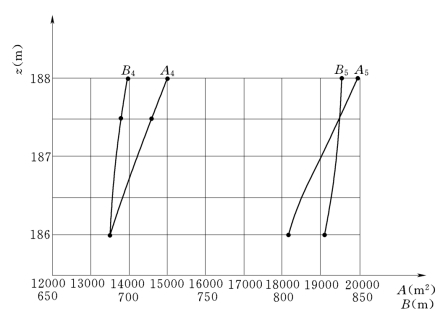
图7.7.3

当z=186.65m 时，从上图中查得 （或内插计算）A5=18685m2，B5=832m，又Δs4-5=6000m，Q=26500m3/s，n=0.04，ζ4=0。于是：

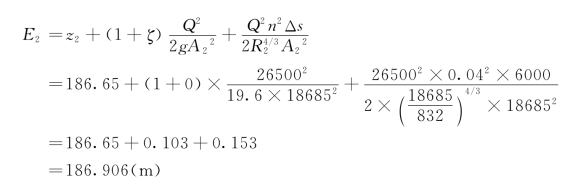
假设z4=187m，则A4=14200m2，B4=690m。于是：

假设z4=187m，计算出的z4=187.025m，两者相差只有2.5cm，这对于试算方法精度已足够了，故对此断面不再继续试算，取两者之中哪一个值均可。用类似的方法可以求得z3、z2及z1。当然，试算范围的选取需要经验，同时这种试算也是相当麻烦的。如果采用电算，将很容易得到计算结果。