对于非棱柱形渠道，如溢洪道陡槽中的收缩段和扩散段，其过水断面面积随水深和距离而变化，即A=f（h，s），因此在微段计算中只假设水深就不够了，同时还要先划分好微段距离。这时对于每个微段都要采用试算法，其步骤如下。

（1）根据与非棱柱形渠道相接的棱柱形渠道中水面曲线的分析，先找出控制断面或计算起始断面的水深hs。

（2）将非棱柱形渠道分成若干个微段Δs。

（3）如果令hu=hs（意味是急流，否则令hd=hs），计算Au、vu、Xu、Ru、Cu及Jfu。

（4）根据已知的Δs和假设的水深hd，计算Ad、vd、Xd、Rd、Cd及Jfd。

（5）根据式（7.6.6）计算Jf，根据式 （7.6.4）计算Δs，如果算出的Δs与已知的Δs不相等，需重新假设hd，直到算出的Δs与已知的Δs相等为止。然后将此微段的hd作为下一微段的hu，重复步骤（3）～ （5），依此类推，逐段计算。

例7.6.1 如图7.6.2所示，为一水库正堰式溢洪道，其设计流量Q=300m3/s，水流由宽顶堰流入，经过渐变段后由陡槽末端挑出。整个溢洪道均为混凝土矩形断面，粗糙系数n=0.014。宽顶堰处的底坡i0=0，渐变段长度s1=20m，始端底宽b1=20m，末端底宽b5=15m，底坡i1=0.15。陡槽长度s2=100m，底坡i2=0.20，试用分段求和法计算全溢洪道中的水面曲线。

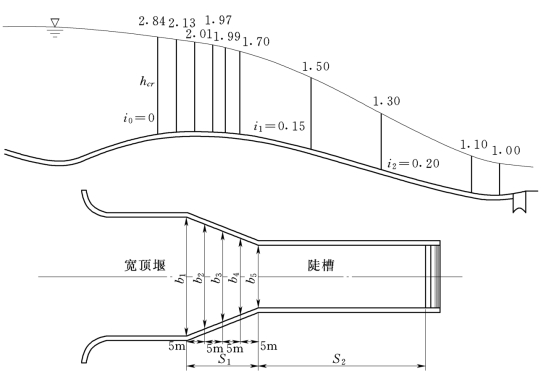
图7.6.2

解：

（1）渐变段中的水面曲线计算

由于渐变段和陡槽均为陡坡，所以由宽顶堰进入渐变段处的水深为临界水深hcr，水面曲线计算由此处开始向下游进行。应用的公式为：

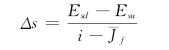
而

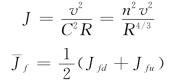
将渐变段分成四段，各段长度均为5m，相应的底宽分别为20m、18.75m、17.5m、16.25m及15m。

第一微段计算，这时h1=hcr，b1=20m。

单宽流量

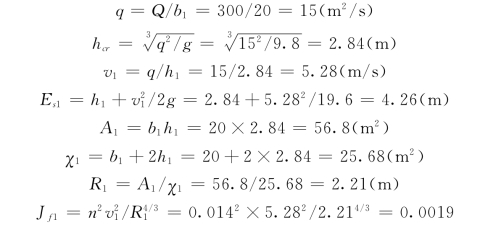
设h2=2.15m，则

(www.daowen.com)

所以

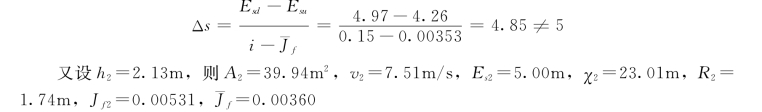
所以

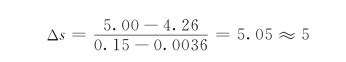
第一微段计算结束，将h=2.13m作为第二微段的h1，依次计算下去，见表7.6.1。最后得各断面水深分别为2.84m、2.13m、2.01m、1.97m及1.99m。

表7.6.1

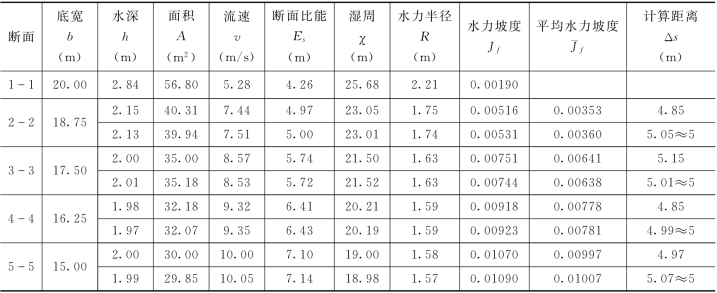
（2）陡槽中的水面曲线计算

采用水深法判别底坡的陡缓。

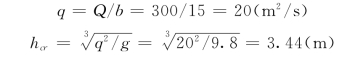
此题不能用图解法求正常水深，因为超出了图中的数据范围，只能采用试算法。

设h0=0.79m，则A=0.79×15=11.85 （m2）

接近于671，故取h0=0.79m。因为h0＜hcr，所以为陡坡渠道。又知上游端水深为h2=1.99m，大于h0小于hcr在b区，因此产生b2降水曲线。

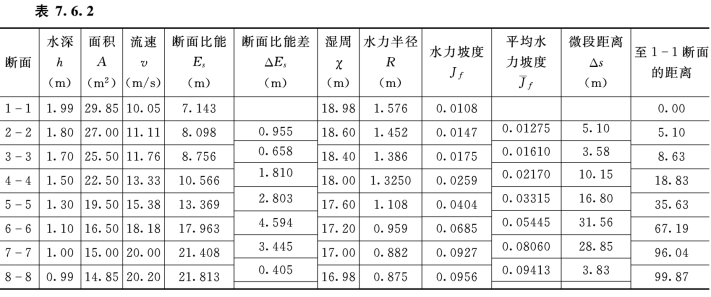
陡槽中的水面曲线计算见表7.6.2。