定性分析水面曲线有以下两个任务：

（1）根据已知水深h在具体渠道中所处的区，确定水面曲线的类型，是壅水曲线还是降水曲线，是哪种类型的壅水曲线和哪种类型的降水曲线。

（2）指出d h/d s的极限情况，即水面曲线两端的变化趋势。

下面对五种底坡，根据h与h0、hcr之间的关系，用式 （7.4.3）～式 （7.4.5）进行具体的水面曲线分析。正底坡用式 （7.4.3），平底坡用式 （7.4.4），反底坡用式（7.4.5）。

1.i＜icr（h0＞hcr）的情况

（1）水深在a区，h＞h0＞hcr。

因为h＞h0，所以i-Jf＞0；因为h＞hcr，所以E′s＞0，由式（7.4.3）得：

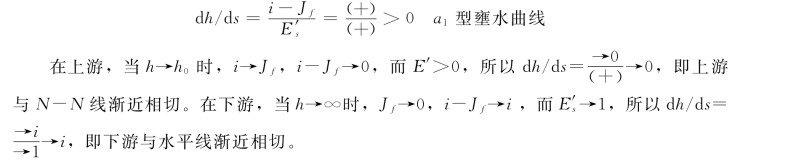
（2）水深在b区，hcr＜h＜h0。

因为h＜h0，所以i-Jf＜0；因为h＞hcr，所以E′s＞0，故

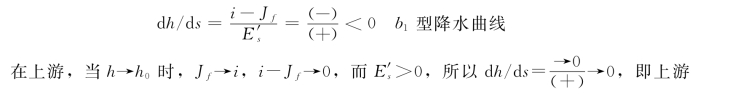
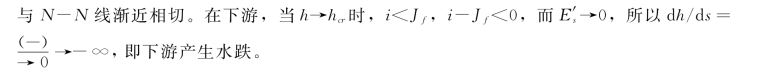
（3）水深在c区，h＜hcr＜h0。

因为h＜h0，所以i-Jf＜0；因为h＜hcr，所以E′s＜0，故

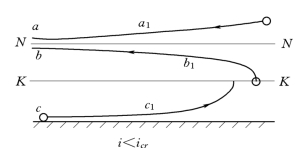
图7.5.2

正底坡i＜icr时的三种水面曲线如图7.5.2所示。

2.i＞icr（hcr＞h0）的情况

（1）水深在a区，h＞hcr＞h0。

因为h＞h0，所以i-Jf＞0；因为h＞hcr，所以E′s＞0，故

(www.daowen.com)

（2）水深在b区，hcr＞h＞h0。

因为h＞h0，所以i-Jf＞0；因为h＜hcr，所以E′s＜0，故

（3）水深在c区，hcr＞h0＞h。

因为h＜h0，所以i-Jf＜0；因为h＜hcr，所以E′s＜0，故

在底坡中i＞icr时的三种水面曲线如图7.5.3所示。

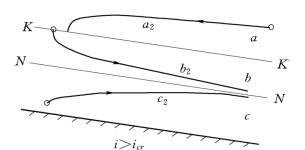
图7.5.3

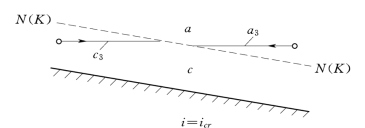
图7.5.4

3.i=icr（h0=hcr）的情况

在此种情况下，因为h0=hcr，N-N 线与K-K线重合，即没有b区，只有a区和c区，也即只有a3型和c3型水面曲线。又由于i=icr介于i＜icr和i＞icr之间，所以a3型曲线的变化规律介于a1和a2之间，c3型曲线的变化规律介于c1和c2之间，即a3和c3曲线只能是两条水平线，如图7.5.4所示。

4.i=0的情况

对于i=0的情况，不存在正常水深h0，即没有N-N 线，也就不存在a区，只存在b区和c区，故只能产生b0和c0水面曲线。水面曲线分析用式 （7.4.4），分析方法同前，故省略。b0型水面曲线是降水曲线，上游与水平线渐近相切，下游水深h接近hcr时产生水跌。c0型曲线是壅水曲线，上游始于某一控制水深，如hc。下游水深h接近hcr时产生水跃。b0和c0曲线如图7.5.5所示。

5.i＜0的情况

对于i＜0的情况，同样不存在正常水深h0，即没有N-N 线，也就不存在a区，只有b区和c区，故只能产生b′和c′水面曲线。水面曲线分析用式 （7.4.5），分析方法同前，故省略。b′型水面曲线也是降水曲线，上游与水平线渐近相切，下游水深h接近hcr时产生水跌。c′型水面曲线也是壅水曲线，上游始于某一控制水深，如hc。下游水深h接近hcr时产生水跃。b′和c′曲线如图7.5.6所示。

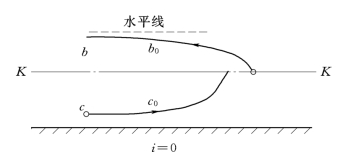
图7.5.5

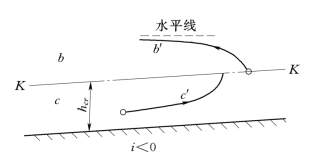
图7.5.6