水面曲线定性分析用到的基本公式是式（7.4.3）、式 （7.4.4）及式（7.4.5）。

下面先说明上面三式中左端取得不同值时的几何意义：

d h/d s＞0时，水深沿程增加，产生雍水曲线；

d h/d s＜0时，水深沿程减小，产生降水曲线；

d h/d s→0时，水深趋于正常水深，即水面线与均匀流水面线渐近相切；

d h/d s→+∞时，水深突然增大，即渠中产生水跃；

d h/d s→-∞时，水深突然减小，即渠中产生水跌；

d h/d s→i时，水面线与水平线渐近相切。

式 （7.4.2）可以写成为：

(www.daowen.com)

式中K0与h0有关，K 与h 有关，即左端分子与i及h0/h有关；分母的正负号取决于hcr/h：hcr/h＞1时为急流，Fr＞1，分母为负；hcr/h＜1时为缓流，Fr＜1，分母为正。所以式（7.4.3）～式 （7.4.5）可统一写成下面函数形式：

式 （7.5.2）说明，对于一定底坡的棱柱形渠道中的恒定渐变流，其水深沿程的变化规律与正常水深h0与水深h之比，临界水深hcr与水深h之比有关。因此在具体分析水面曲线以前，需先将渠底以上的空间以hcr的轨迹线K-K和h0的轨迹线N-N 分成a、b、c三个区：N-N 线与K-K线以上的区域为a区；N-N 线与K-K 线之间的区域为b区；N-N 线与K-K线以下的区域为c区。

由7.1节可知，渠道底坡分正底坡、平底坡和反底坡三种。而正底坡渠道又包括缓坡、陡坡和临界坡。在缓坡和陡坡渠道中，正常水深和临界水深都存在，即N-N 线和K-K线都存在，因此各有a、b、c三个区；在临界坡渠道中，因为正常水深与临界水深相等，即N-N 线与K-K线重合，所以没有b区，只有a、c两个区。在平底坡和反底坡渠道中，没有正常水深，即没有N-N 线，只有K-K 线。这时可以理解为h0为无穷大，即N-N 线位于无穷远处，相当于排除了a区，故只剩下b、c两个区。这样，五种底坡的渠道中共有12个区，如图7.5.1所示，每个区中有一条水面曲线，共有12条水面曲线类型。五种底坡中的水面曲线依次加脚标1、2、3、0，以示区别，例如正底坡a区的水面曲线为a1，平底坡b区的水面曲线为b0，反底坡c区的水面曲线为c′等。

为了分析式 （7.4.3）～式 （7.4.5）右端的取值情况，先分析Jf和E′s（E′s=d Es/d h）随水深变化的取值情况：

均匀流（h=h0）时，i=Jf，即i-Jf=0；

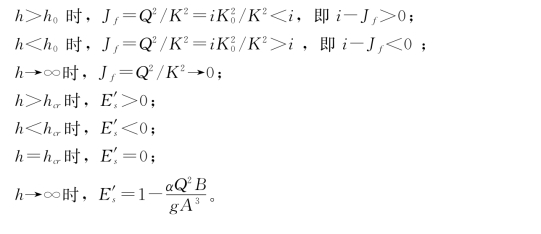
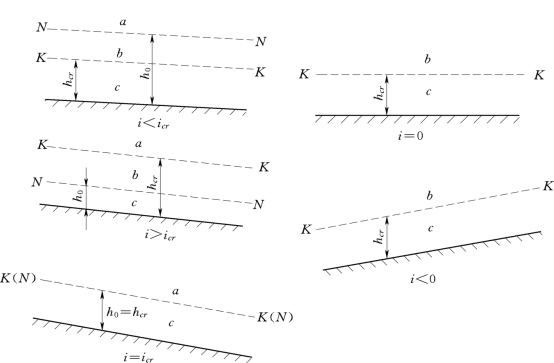
图7.5.1