为了定性分析水面曲线和定量计算水面曲线，需要先建立明渠恒定渐变流的基本微分方程。

如图7.4.1所示，在明渠恒定渐变流中取相距d s的两过水断面1-1和2-2，1-1断面到某起始断面的距离为s。设1-1和2-2断面渠底到基准面0-0的距离、水深、断面平均流速分别为z、h、v和z+d z、h+d h、v+d v。又设渠中流量为Q，底坡为i，两断面的动能校正系数α1=α2=α=1，忽略两断面间的局部水头损失d hj，则d hw=d hf。以0 0为基准面，写两个断面的能量方程，并注意到：d z=-i d s；用均匀流公式近似地计算非均匀流中的沿程水头损失，设均匀流的流量模数为K，则d hf=Q2d s/K 2；忽略（v+d v）2/2g展开后的二阶微量（d v）2/2g，则得：

化简后得：

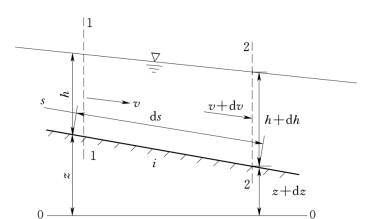
图7.4.1

注意到Es=h+v2/2g，最后得：

式 （7.4.1）就是明渠恒定渐变流的基本微分方程。但是，为了定性分析水面曲线和定量计算水面曲线，还要将它变成水深h与距离s之间的函数关系。我们在7.2节中已得出式（7.2.8）：

(www.daowen.com)

由式（7.2.8）除以式（7.4.1），得：

式 （7.4.2）是明渠恒定渐变流的基本微分方程的另一种表达形式。此式反应了明渠水流水深的沿程变化规律。

式 （7.4.2）是对正底坡渠道而言的。又知Q 2/K 2=Jf，Jf为渠中的水力摩阻坡度。令d Es/d h=E′s，E′s是断面比能对水深的导数。于是式（7.4.2）又可以写成为：

对于平底坡渠道i=0，所以有：

对于反底坡渠道i＜0，可以将i写成为-|i|，所以有：