在水利工程中经常遇到由急流向缓流过渡的情况,如图7.3.2所示的闸孔出流的下游,靠近闸门附近的流动是急流,而下游渠道中的流动是缓流,这时从急流向缓流过渡也经过临界水深hcr,但是根据7.4节对非均匀流水面曲线的分析可以知道,此时临界水深前后的水面不可能像水跌那样平顺衔接,而必然会发生不连续的水面衔接方式,因而有水面突然升高的局部水力现象,此现象称为水跃。溢流坝的下游也会发生类似的现象。
水跃由表面水滚和其下面的主流组成。表面水滚是若干具有水平轴的漩涡的集合体。由于漩涡的旋转、摩擦、冲击及其与主流之间的动量交换将上游急流的动能消除一部分,因此水跃有消能作用。
水跃前端和后端的断面分别称为跃前断面和跃后断面,其过水断面面积记为A1和A2,跃前断面和跃后断面的水深称为跃前水深和跃后水深,记为h′和h″,跃后水深与跃前水深之差称为水跃高度,记为a,a=h″-h′;跃前断面与跃后断面之间的水平距离称为跃长,记为lj,跃前水深h′与跃后水深h″称为彼此的共轭水深。
我们本节的主要任务就是建立共轭水深之间的关系。由于水跃中的能量损失尚不知道,因此将应用动量方程。取如图所示的1-1、2-2断面间水体为控制体。假设:
(1)底坡水平。
(2)水跃较短,忽略渠床对水体的摩擦力作用。
(3)两个断面上的动量校正系数α01=α02=1。
(4)1-1和2-2断面是渐变流断面,因此两断面上的动水压强分布规律与静水压强分布规律相同,即P=γycA,式中yc是过水断面的形心在水面下的深度。
根据上面的假设,x方向的动量方程为:
![]()
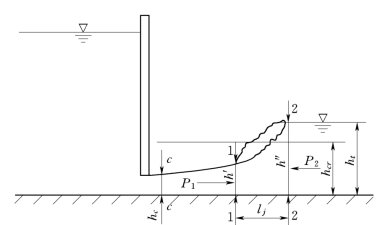
图7.3.2
式中 yc1、yc2——A1和A2的形心在水面下的深度。
注意到上式中v2=Q/A2,v1=Q/A1,移项整理后得:
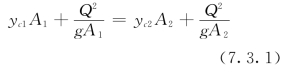
式 (7.3.1)就是平底坡棱柱形渠道的水跃基本方程。
因为式(7.3.1)中的y、A均是水深h的函数,其余量均为常数,所以可写出下式:
![]()
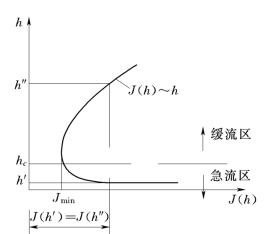
图7.3.3
J(h)称为水跃函数,类似断面比能曲线可以画出水跃函数曲线,如图7.3.3所示。该曲线上对应水跃函数最小值的水深是临界水深hcr;当h>hcr时,J(h)值随水深的增大而增大;当h<hcr时,J(h)值随水深增大而减小。
这样,式 (7.3.1)可写为:
![]()
此式说明共轭水深h′、h″是使水跃函数值相等的两个水深,在图7.3.3上就是同一条铅垂线与水跃函数曲线相交两点所对应的水深。同时从图上也可以看出,跃前水深越小对应的跃后水深越大。
对于矩形断面渠道,式 (7.3.1)中的yc1=h′/2,yc2=h″/2,A1=bh′,A2=bh″,Q=bq,q为单宽流量,整理后得:
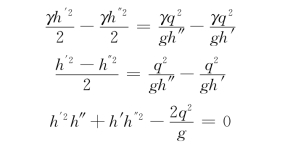
此式是关于h′、h″的一元二次方程,其解为:

假设下游渠道的水深为ht,如图7.3.4所示的闸下收缩断面c-c的水深为hc,hc的共轭水深为h″c,则根据ht与h″c的对比关系闸门下游可能会产生三种不同的水跃。
(1)当ht<h″c时,产生远驱式水跃。这是因为跃后水深只能是ht,ht小要求的跃前水深就要大,这时只有水跃前驱,在收缩断面c c之后产生一段壅水曲线,当壅水深度与ht共轭时才能产生水跃,如图7.3.4中的①。
(2)当ht=h″c时,产生临界式水跃。因为这时ht与hc共轭,跃前断面就发生在收缩断面c c处,如图7.3.4中的②。
(3)当ht>h″c时,产生淹没式水跃。这是因为跃后水深只能是ht,ht大要求的跃前水深就要小,但是跃前水深最小也只能是收缩断面水深hc,其结果是动水压力较大的下游水体将水跃压向闸门,使收缩断面c c被淹没,如图7.3.4中③所示。
矩形断面水平底坡渠道中自由水跃的长度lj一般是由下面的经验公式确定。(https://www.daowen.com)
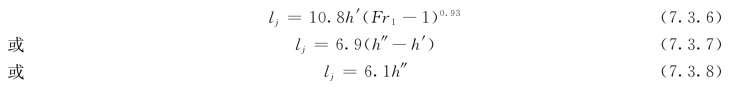
式 (7.3.8)只适用于4.5<Fr1<10。
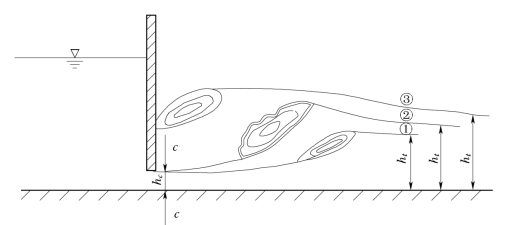
图7.3.4
跃前断面与跃后断面单位重量水体的总机械能之差定义为水跃中消除的能量,记为ΔEj。假设跃前与跃后断面的水深和流速分别为h′,v1和h″,v2,则
![]()
水跃的消能功率为:
![]()
我们将水跃中消除的能量与跃前断面单位重量水体的总机械能之比定义为水跃的消能系数,记为Kj,则

当4.5<Fr1<9.0时,水跃稳定,消能效率也高,Kj=45%~70%,跃后水面也较平稳。
底坡等于0的非矩形断面渠道中的水跃共轭水深计算公式也可以从式 (7.3.1)导出,这里就不赘述了。
例7.3.1 如图7.3.5所示,为一在平底坡段上的平板闸门下出流,已知闸孔下泄的单宽流量q=7.00m2/s,收缩断面c c处的水深hc=0.70m,下游渠道中的水深ht=3.45m,收缩断面下游渠道宽度b=4m,试求:
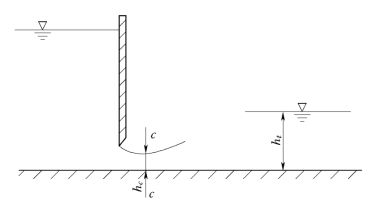
图7.3.5
(1)判别闸下游发生水跃的类型。
(2)该水跃的长度。
(3)该水跃的消能功率及消能系数。
解:
(1)水跃类型判别
hc的共轭水深为:
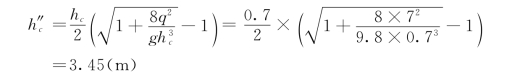
因为ht=h″c=3.45m,所以产生临界式水跃。
(2)水跃长度
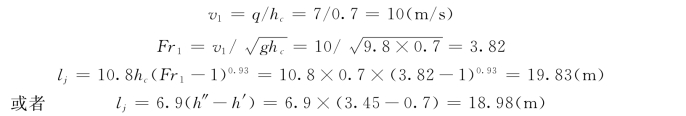
(3)水跃的消能功率及消能系数
水跃中消除的水头为:
![]()
水跃的消能功率为:
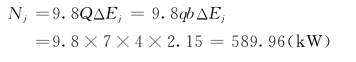
水跃的消能系数为:
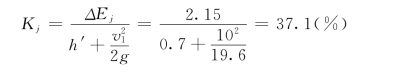
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





