明渠均匀流计算中最基本的公式是谢才公式和曼宁公式，即

其中：

从而流量为：

或者

式中 K——流量模数，相当于i=1时的流量，K = AC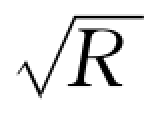，m3/s；

n——边壁粗糙系数，见表7.1.2。

在均匀流渠道的设计中，有时还应用到水力最佳断面的知识。这是指在流量、底坡、粗糙系数已知时，要求设计的过水断面具有最小的面积；或者说，在过水断面面积、底坡和粗糙系数等已知时，能使渠道通过的流量最大，这种断面就是水力最佳断面。

由于均匀流渠道中的流量为：故从此式中可以看出：当渠床的粗糙系数n、底坡i及过水断面面积A 一定时，湿周X愈小流量Q 愈大。根据以上所述，圆形或半圆形应是水力最佳断面，但在天然土质渠道中，采用圆形或半圆形断面是不可能的，而梯形断面是工程上最常采用的形式。下面就以常用的梯形断面为例，推求水力最佳断面时宽深比b/h与边坡系数m 之间的关系。

表7.1.2

根据前述，水力最佳断面的条件为A等于常数和湿周X最小，即d X/d h=0。由梯形断面渠道的几何关系，得：

从中解得：

代入湿周关系式中得出：

则

将A=bh+mh 2代入上式，并令d X/d h=0，则得：

令b/h=βm，βm 是水力最佳断面的宽深比，最后得：

式 （7.1.6）中取边坡系数m=0，即得最佳矩形断面的宽深比：

式 （7.1.6）只是从水力学角度出发而导出的，一般只适用于流量或水深较小的渠道，否则按此式设计出的渠道会成为窄深式，这时既不易施工，且造价也会升高。所以一条渠道的设计除了考虑水力最佳条件以外，还要结合具体情况考虑经济等其他方面的多种因素。(www.daowen.com)

均匀流有以下几种解法。

1.直接解法

（1）当其他量已知，求流量Q或底坡i或粗糙系数n时，可直接由式（7.1.4）解得。

（2）对于宽矩形断面渠道求正常水深时，也可以直接求解。在水力学中称均匀流水深为正常水深，记为h0。因为对于宽矩形断面渠道，水力半径R≈h0，A=bh0，若令q=Q/b，q是单宽流量，代入式（7.1.4）后，得：

所以

（3）当已知渠道的宽深比时，也可以直接求解渠中的正常水深。梯形断面渠道的过水断面面积为：

湿周为：

将A和X代入式（7.1.4）后，得：

令β=b/h0，β为渠道的宽深比，将b=βh0代入上式，得：

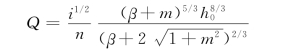
所以

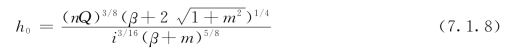
或者

2.试算法或图解法

（1）当已知Q、i、n、m、b （或h0）求h0（或b）时，理论上是可以由式 （7.1.4）求解的，但是，由于此式是h0和b的隐函数，因此不能直接求出它们，只能采用试算法，或者应用附图Ⅰ的图解曲线求解。试算法是从小到大假设一系列水深h1，h2，… （或者底宽b1，b2，…），计算相应的流量Q1，Q2，… （或者流量模数K1，K2，…），然后以水深h （或b）作为纵坐标，流量Q （流量模数K）作为横坐标，绘出h～Q （或K）或b～Q （或K）曲线，最后从曲线上找出对应已知Q （或K）的水深h0（或底宽b）即为所求，示意图如图7.1.5所示。

图7.1.5

（2）当已知宽深比β=b/h0或者最佳宽深比βm，可以用附图Ⅰ图解曲线求解。

3.联解

当限制渠中流速v和水深h0（或b）求底坡i和底宽b （或h0）时，或当限制渠中流速v和底坡i求水深h0和底宽b时，这两种情况均需补充下面方程式：

然后与式（7.1.4）联解。