进行环状管网水力计算时，通常是根据工程要求已经确定了管线布置。因此各管段的长度和各节点的流出流量是已知的。这样，环状管网水力计算的任务是确定各管段通过的流量和各管段的直径d，进而求出各管段的水头损失hf及节点水头。有了水头损失hf再根据控制点的地面标高和所需的自由水头以及总水头损失，即可推求水塔高度。

研究任一环状管网，可以发现管网的管段数目ng和环数nk及节点数目np存在下列关系：

如果能够列出ng个方程，就可以解出ng个管段所通过的流量。

根据环状管网的水流特点，对其水力计算提供了以下三个条件。

（1）根据连续性条件，在各个节点上，流向节点的流量应等于由此节点流走的流量。如以流向节点的流量为正值，离开节点的流量为负值，则两者的和应该等于零，即在各节点上：

通常称该方程为水量平衡方程。

（2）对任一闭合的环路，由分流节点沿不同管线流向汇流节点的水头损失应相等（这相当于并联管路中，各并联管段的水头损失应相等）。因此，在任一环路内，如以顺时针方向水流所引起的水头损失为正值，逆时针方向水流的水头损失为负值，则任一闭合环路内的水头损失的代数和应等于零，即在各环内：

式中 hfi——环内某一管段的沿程水头损失；

S0i——环内某一管段的比阻；

Qi——环内某一管段通过的流量；

li——环内某一管段的长度。

根据第一个水力条件，可列出（np-1）个

的方程式，对每个节点均有独立的水量平衡方程∑Qi=0，但不包括最后一个节点。

根据第二个水力条件，可列出nk个

的方程。

对环状管网共可列出（nk+np-1）个方程，方程数目正好等于管段数。但每个管段有流量Q和管径d两个未知数，总未知数共有2 （nk+np-1）个。因此在实际计算时，有时参照经济流速确定管径，从而使未知数减少一半。这样未知数的数目和方程的数目一致，方程就有确定解。

工程上，多采用逐次近似方法求解环状管网，具体步骤如下。

（1）首先按各节点供水情况初步拟定各管段的水流方向，通常整个管网的供水趋势应指向大用户集中的节点，并按每一节点满足：

的条件，第一次分配各管段通过的流量Qi（脚标i表示i管段中的量）。

（2）按所分配流量，参照经济流速确定各管段直径，即

并按初步分配的流量Qi和管径di计算各管段的水头损失，即

（3）校核每一环路的水头损失之和，即

是否等于零，如不等于零，说明初步分配的流量不满足环状管网的第二个水力条件，需对第一次分配的流量进行调整。

当最初分配的流量，不满足每一环路内的水头损失之和等于零时，即称为不满足闭合条件，应在所计算的环路中加入校正流量ΔQ，下面推导校正流量ΔQ的方程。

设最初分配的流量不满足闭合条件，令

式中 Δh——闭合差。(www.daowen.com)

若令校正流量为ΔQ，则校正后的单环闭合差应为零，即

将式（6.4.4）改写为：

然后将上式按二项式展开，取前两项，则得：

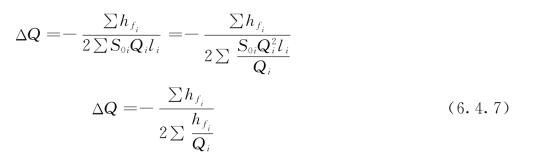
由此解得：式中Qi与hfi应取一致符号，规定环内水流以顺时针方向流动为正，逆时针方向流动为负。

将校正流量ΔQ与环内各管段第一次分配的流量相加得各管段第二次的分配流量，再按上述步骤重复计算，直至环内闭合差Δh满足所允许的误差为止。

上面所介绍的方法也称为哈迪—克劳斯（Hardy-Croos）方法。

近年来，随着电子计算机进行管网计算愈来愈广泛，特别是对多环管网，更显示了既准确又迅速的优越性。关于这方面的知识可参看本书附录。

图6.4.4

例6.4.2 有一环状管网的管长、管段编号及节点分出流量如图6.4.4所示，管道为铸铁管，允许的单环闭合差Δh=0.25m。试求各管段通过的流量和管径。

解：

计算步骤如下：

1）按管网供水趋势指向大用户集中的节点，初拟管网水流方向，并按节点水量平衡条件

∑Qi=0第一次分配环内各段流量列于表内。

2）按经济流速确定管径：

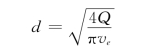
以管段①为例，初拟流量Q为90L/s，经济流速ve采用1.2m/s，则

选取接近的d=300mm。

其余各管段计算结果列于表中。联结管③和管⑤的管段，采用的管径比计算值稍大些，因为当干管损坏时，管③和管⑤要输送较大流量到被损坏的管段以后的地点。

3）按管径由表6.3.2得各管段比阻S0i，并计算相应各管段的水头损失hfi。仍以管段①为例：

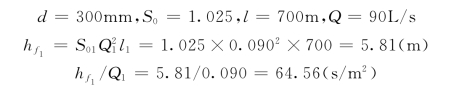
将其余各段计算结果列于表6.4.2中。

4）计算各环路的闭合差。以第Ⅰ环路为例：

闭合差Δh=1.68 （m）＞ε=0.25m，应重新进行流量分配。

按上述步骤，重复计算，直到闭合差满足允许的精度。本例题第四次计算的最大闭合差Δh=0.225m＜ε=0.25m，不再进行计算，以第四次分配的流量为各管段的流量Q。

表6.4.2