枝状管网是由多条管段串联而成的干管和与干管相联的多条支管组成，如图6.4.1（a）所示。它的特点是管网内任一点只能向一个方向供水。若在管网内某一处出现故障，那么该点后面各管段供水就出现断流，因此枝状管网供水可靠性差，但节约管材，造价低是其优点。

枝状管网的设计，一般是先根据工程要求、建筑物布置、地形条件等进行整个管线的布置，确定各管段长度和通过各管段的流量以及管段末端要求的剩余水头Hs（也称自由水头），然后确定各管段的直径d和水塔应有的高程（水泵扬程）。

一般取距水源远、地形高、建筑物层数多、流量大的供水点为最不利点或控制点。把水塔到控制点的管段作为干管，其余为支管。由于干管是由通过不同流量、不同管径的管段串联而成，因此枝状管网可按串联管路计算。

图6.4.2

计算时，首先在已知流量下参考经济流速选择管径，按式 （6.3.3）或式（6.3.4）：

计算各段的水头损失。然后按串联管路计算从水塔到管网的控制点的总水头损失。设水塔水面距地面的高度为Ht，如图6.4.2所示，则水塔高度Ht为：

式中 Ht——水塔高度；

∑hf——从水塔到管网控制点的水头损失；

Hs——控制点的剩余水头；

z0——控制点的地形标高；

zt——水塔处的地形标高。

若水塔已经建成，要求扩建已有的给水系统。这种情况相当于已知总水头H、管线布置图和各管段通过的流量，需求管径d。此时，在水头已确定的情况下，如果用经济流速确定管径，将不能保证供水要求。一般可按下面介绍的方法确定支管的管径。

支管起点的水头，由于干管上各节点的水头已求出，所以是已知的。支管终点的水头则根据工程要求、终点地面高程等确定。

当支管起点、终点水头及管长已确定后，可按下式求出任一支管的平均水力坡降：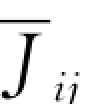

式中 Hi——同一支管起点水头；

Hj——同一支管终点水头；

lij——该支管的长度。

由支管的平均水力坡降Jij及该支管通过的流最Qij，可由式 （6.3.4）求得该支管的比阻S0ij：

由上式求得比阻S0ij值后，可由舍维列夫公式最终求出该支管管径。(www.daowen.com)

例6.4.1 一枝状管网从水塔A沿A 1线向各处输送用水，各节点要求供水量如图6.4.3所示。已知每一段管路长度（表6.4.1）。地面标高：水塔处为65m，点4为70m，点7为71m。点4和点7要求的自由水头Hs为2m，试求各管段的直径、水头损失及水塔应有的高度Ht。

解：

根据经济流速选择各管段的直径，例如对于3-4管段Q=25L/s，采用经济流速ve=1m/s，则管径为：

管中实际流速：

图6.4.3

采用铸铁管，由表6.3.2得比阻S0=9.029。因平均流速v=0.8m/s＜1.2m/s，比阻S0应修正。当v=0.8m/s，查表6.3.3得修正系数k=1.06，则3-4管段的水头损失：

各管段的计算见表6.4.1。

表6.4.1

从水塔到最远的用水点4和7的沿程水头损失分别如下。

沿4-3 2-1-A线为：

沿7-6 5-1-A线为：

点7相对水塔的地面高差为： 71-65=6（m）

点4相对水塔的地面高差为： 70-65=5（m）

最后选定点7为控制点。总水头损失∑hf=7.94m，自由水头Ht=12m，相对标高z=6m，则A点的水塔高度为：

取水塔高度Ht为26m。