复杂管路是由多条简单管路组成的。按布置的不同可分为串联管路、并联管路、分叉管路、管网等。下面将分别加以介绍。为便于分析，假定流动均在阻力平方区。

1.串联管路

由直径不同的管路依次连接而组成的管路，称为串联管路，如图6.3.3所示。串联管路常用于向各处供水，经过一段距离就有一定的流量分出，图中q1、q2即为分出的流量。随着流量的减少，所采用管径也相应减小。有时流量虽然不变，但为了节约钢材，充分利用水头，也采用串联管路，即将不同管径的管段串联起来。

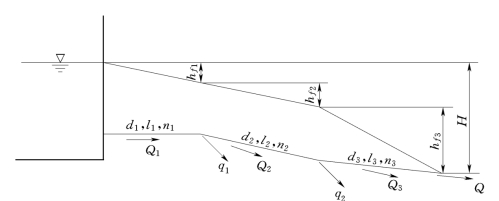
图6.3.3

串联管路各管段虽然串联在一个管路系统中，但因各管段的管径、流量、流速各不相同，所以应分段计算其沿程水头损失。

设串联管路各管段长度、直径、管中流量及各段末端分出的流量分别用li、di、Qi、qi表示。串联管路总水头损失等于各管段水头损失之和，即串联管路的总水头为：

或

式中 n——管段总数目。

串联管路的流量计算应满足连续方程，即

式 （6.3.8）～式 （6.3.10）是串联管路水力计算的基本公式。

与简单管路一样，利用这三个公式可以解决串联管路水力计算中的三类基本问题，即确定输水能力、确定总水头或者确定管径。

串联管路的测压管水头线与总水头线是重合的。由于各管段流速不同，所以水力坡度不相同，因此整个管路的总水头线呈折线形，如图6.3.3所示。

例6.3.2 某工厂管路系统如图6.3.2所示。若水塔向工厂供水的流量为40L/s，水塔水面距地面的高度H1为44m，水塔与工厂地面标高差zt为16m，管路末端剩余水头H2为25m，管线全长l为2500m。为了充分利用水塔的水头和节省钢材，决定采用管径d为300mm和d为200mm的两种管道串联，求每根管道的长度l1和l2。

解：

设d1=300mm，管长为l1，d2=200mm，管长为l2。

管中流速：

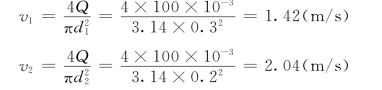
查管道流量模数系数表6.3.1得：

当d=300mm时，K1=1.006×103L/s；

当d=200mm时，K2=34.1L/s。

代入式（6.3.8）得：

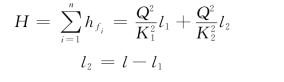
由能量方程得：

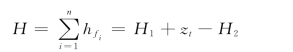
将已知数据代入，则有：

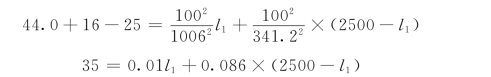
解得：

最后采用管径d=300mm的管段长为2367m，d=200mm的管段长为133m。

2.并联管路

两条或两条以上管段从一点分叉又在另一点汇合的管路称为并联管路，管段分叉或汇合点称为节点。如图6.3.4所示，A、B为节点。如在A、B两点安装测压管，由于是长管，测压管水头差可视为总水头差，测压管内水面差就是A、B两点之间的水头损失hfAB。单位重量的液体通过AB之间任意一个管段水头损失都是相等的。即并联管路中的每一管段两端的水头差都是相等的，这就如同并联电路中每一导线两端的电压差都是相等的一样。若以hf1、hf2、hf3分别表示并联管路各管段的水头损失，则有：

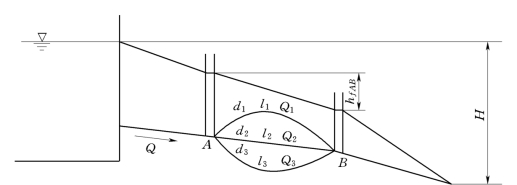
图6.3.4

由式（6.3.3），得并联管路各管段的水头损失为：

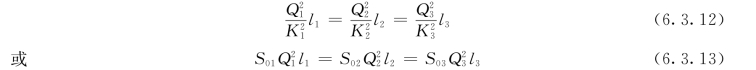
因并联管路各管段直径、长度、粗糙系数可能不同，所以，虽然水头损失相同，但通过的流量却会是不同的，各管段的流量与总流量应满足连续方程，即

式 （6.3.12）～式 （6.3.14）是并联管路水力计算的基本公式。若已知Q及各并联管段的直径、长度和粗糙系数，由以上三式联立求解，可得到各管段的流量Q1、Q2、Q3及并联管路水头损失hfAB。

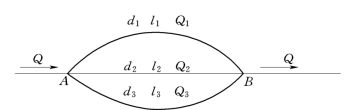
图6.3.5

例6.3.3 三根并联铸铁管路由节点A分出，在节点B汇合，如图6.3.5所示。已知Q=280L/s，d1=300mm，l1=500m，d2=250mm，l2=800m，d3=200mm，l3=1000m，各管段的粗糙系数n均为0.0125。试求并联管路各管段的流量Q1、Q2、Q3及水头损失hfAB。

解：

由题意，根据并联管路水力计算的基本公式可得：

将已知数据分别代入上式，得：

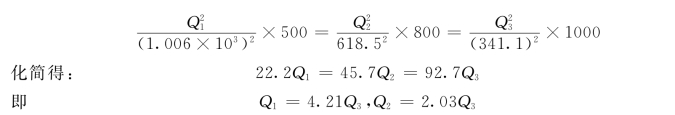
将Q=280L/s代入连续方程Q=Q1+Q2+Q3中，化简得：

AB间水头损失为：

3.分叉管路

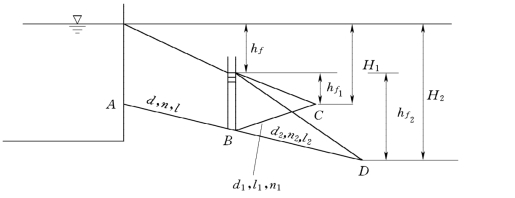
由主干管段分出两条及两条以上支管，分叉后不再汇合的管路称为分叉管路。如图6.3.6所示为一分叉管路。主干管自水池引出后，在B点分叉，支管为BD 和BC。由A点至任一分叉的支管都可看作为一串联管路，所以分叉管路的水力计算可按串联管路计算。设AB、BC、BD管段的水头损失分别为hf、hf1、hf2。流量分别为Q、Q1、Q2。

(www.daowen.com)

图6.3.6

对ABC管路应有：

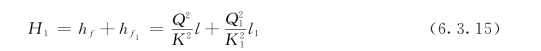
对ABD管路应有：

若按比阻计算，可写成下列形式：

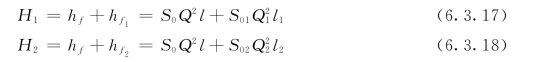
满足连续性方程，应有：

若管道的基本参数都是已知的，联立求解式（6.3.15）、式 （6.3.16）和式（6.3.19）三个方程，就可以求得Q、Q1和Q2三个未知数。

例6.3.4 水电站引水钢管在B点分出两个支管，供两台水轮机用水，如图6.3.7所示。干管长l为40m，直径d为400mm，支管BC长l1为55m，直径d1为200mm；支管BD长l2为60m，直径d2为200mm，粗糙系数按清洁管考虑取n为0.011。求各台机组所通过的流量Q1及Q2。

图6.3.7

解：

由式（6.3.15）和式（6.3.16）得：

由连续方程得：

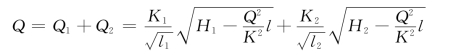
代入已知数据得：

化简得：

采用逐次逼近法，可求得Q=0.452m3/s。

于是

4.沿程均匀泄流管路

给水工程中，有些配水管需沿着管长泄出流量。一般说来，沿程泄出的流量是不均匀的。其中最简单的情况是管路单位长度上泄出的流量均等于q，这种管路称为沿程均匀泄流管路。管路末端流出的流量称为转输流量。

如图6.3.8所示为一均匀泄流管路，设距管末端为x的断面M 处的流量为QM，则

式中 Qt——转输流量；

q——单位长度均匀泄出的流量；

x——该断面距管末端的距离。

由于流量沿程变化，管中水流是非均匀

流，不能直接用均匀流公式计算水头损失。但在M 处取一微小管段d x，由于d x无限小，在这一微小管段中水流可以看作均匀流，可按均匀流公式计算该段沿程水头损失，然后对全管进行积分，即可得整个均匀泄流管路的沿程水头损失。设d x段的流量为QM，则d x管段内的水头损失为：

图6.3.8

式 （6.3.20）可近似写为：

令Qr=Qt+0.55ql，Qr称为折算流量。因此，式 （6.3.21）可以写为：

若转输流量Qt=0，则由式（6.3.20）可得沿程均匀泄流管路的沿程水头损失为：

式 （6.3.24）和式（6.3.25）表明，当流量全部沿程均匀泄出时，即转输流量Qt等于零时，均匀泄流管路的沿程水头损失，只等于全部泄出的流量集中在末端泄出时的沿程水头损失的1/3。

由于沿程均匀泄流管路流量沿程减少，在断面不变的情况下，流速沿程减小，水力坡度J沿程变化，所以总水头线是一条坡度逐渐变缓的曲线。如图6.3.8所示。

图6.3.9

例6.3.5 由水塔供水的输水管路，如图6.3.9所示。全管路包括三段，中间AB为沿程均匀泄流管路，每米长度上连续分泄的流量q=0.1L/s，第一段和第二段管接头处要求泄出流量Q1=15L/s，第三段管末端的流量Qt=10L/s，各管段的长度和直径分别为l1=300m，l2（AB）= 200m，l3= 100m，d1=200mm，d2=150mm，d3=100mm，管路均为铸铁管，试求需要的水头H。

解：

首先求出各管段的流量模数K值，查表6.3.1得：

由式（6.3.8），串联管路的总水头为：

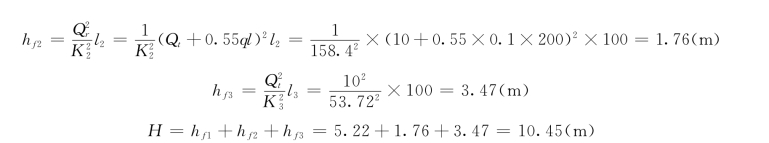
该输水管路所需总水头为10.45m。