紊流流动中,在靠近壁面处由于壁面的约束,流速的横向脉动很小,u′y≈0,故紊流附加切应力τ′≈0,但是,流速梯度d u/d y却很大,故黏滞切应力起主要作用。我们将靠近固体壁面黏滞力起主要作用的作层流运动的极薄层称为黏性底层,其厚度记为δl,如图5.6.1所示。由于黏性底层很薄,故假设其内的流速按直线规律分布。由牛顿内摩擦定律得:
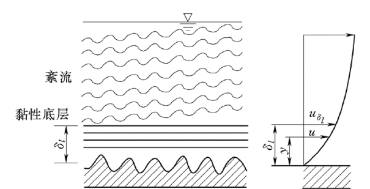
图5.6.1
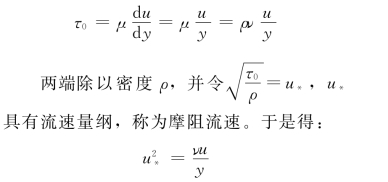
![]()
式 (5.6.1)就是黏性底层中的流速分布公式。
设y=δl时u=uδl,由式(5.6.1)得:
![]()
注意到上式等号右边是以u为特征流速、δl为特征长度的雷诺数,可用以判别黏性底层和紊流的转换点,根据实验分析,在紊流和黏性底层流速分布曲线交点处有:
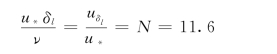
于是

又由式(4.4.9):
![]()
所以

将式(5.6.3)代入式(5.6.2),得:
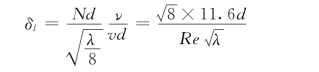
故
 (https://www.daowen.com)
(https://www.daowen.com)
式 (5.6.4)是计算黏性底层厚度的公式。
下面介绍壁面的粗糙度问题。一般工业生产管道(或简称工业管道)的壁面总是凹凸不平的。我们称壁面的凸出高度为壁面的绝对粗糙度,用Δ表示,如图5.6.2 (a)所示。壁面绝对粗糙度的大小、形状及其分布状态制约着其上水流的型态和水流的阻力或水头损失。同一壁面上的不同处绝对粗糙度的大小、形状及其分布状态是不尽相同的,因此说工业管道的绝对粗糙度Δ是一个随机量,也是一个难以确定的量。这样就出现如何表示工业管道壁面的绝对粗糙度问题。水力学中还有一种管道,那就是人工管道。所谓人工管道就是将粒径相同的砂粒均匀的粘在管道壁面上的管道,如图5.6.2 (b)所示。许多管流中的基本规律就是在人工管道中通过实验而得到的,如流速分布规律,沿程水头损失系数λ的变化规律。人工管道壁面上砂粒的直径用ks表示,即人工管道的绝对粗糙度Δ=ks。工业管道的粗糙度是用当量粗糙度ks表示的。所谓当量粗糙度是在水头、管径及管长与工业管道相同的条件下,具有相同的沿程水头损失或沿程水头损失系数时人工管道的绝对粗糙度。通过实验得到的各种工业管道的当量粗糙度见表5.6.1。这样只要将适用于人工管道的各种规律表达式中的粗糙度用工业管道的当量粗糙度ks代替就可以用于工业管道。请注意:在以后的公式中只出现符号ks,对于人工管道它表示砂粒的直径,即绝对粗糙度;对于工业管道,它表示当量粗糙度。
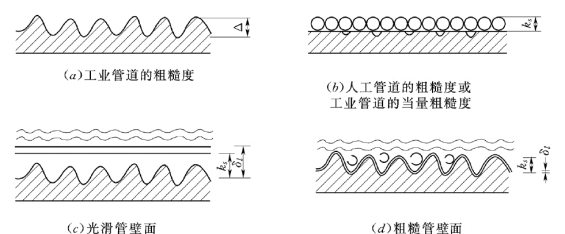
图5.6.2
表5.6.1
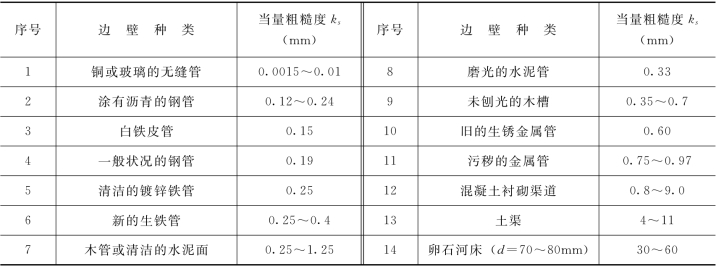
根据黏性底层的厚度σl与当量粗糙ks的对比关系可以将紊流中的壁面分为以下三种:
(1)当δl>ks时,称为水力光滑面,如图5.6.2 (c)所示,若为管道则称为水力光滑管。这时壁面上粗糙突出高度完全淹没在黏性底层的下面,而紊流核在黏性底层上运动,粗糙突出高度对流动没有影响,式 (5.5.12)中右端第一项(黏性切应力)相对第二项(由紊动引起的紊流附加切应力)不是无穷小量,不可忽略。
(2)当δl<ks时,称为水力粗糙面,如图5.6.2 (d)所示,若为管道则称为水力粗糙管。这时壁面上的粗糙突出高度已不能被黏性底层完全淹没,在粗糙突出高度的背后形成许多小漩涡,式 (5.5.12)中右端第二项紊流附加切应力起主要作用,而黏性切应力项相对较小,可以忽略。
(3)介于(1)和 (2)两种情况之间的壁面称为过渡粗糙面,若为管道则为过渡粗糙管。这时壁面的粗糙突出高度仍然被黏性底层完全淹没。但是,在粗糙突出高度的后面并不形成明显的小漩涡,黏性切应力和紊流附加切应力同时起作用。
应当指出:上面的水力光滑管和水力粗糙管是对某一具体管道在一定流量下而言的。当该管道的流量增大后水力光滑管可以变成水力粗糙管;当流量减小后水力粗糙管可以变成水力光滑管。
一般按下述两种指标对紊流进行分区。

式中 ks——壁面的当量粗糙度,可由表5.6.1查得;
δl——黏性底层的厚度,由式(5.6.4)计算;
Re——摩阻雷诺数,可由下式计算:
![]()
而
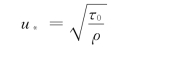
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





