1.紊流附加切应力与脉动流速的关系

由于紊流中液体质点的混掺作用，所以，实际液体中某固定空间点处除具有纵向速度ux以外，还存在横向脉动流速u′y。该横向脉动流速将某一层中的液体搬运到另一层，并与另一层液体相混合。如图5.5.2所示，设在两层液体之间取一微元面积d A，设下层液体的横向脉动流速为u′y，则单位时间内从下层流入上层的液体质量为ρu′yd A。又设下层处的纵向流速为ux=ux+u′x，则在单位时间内流经d A截面的x方向的动量为：

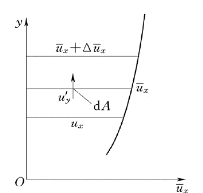
图5.5.2

对上式在相当长一段时间内进行平均，则得动量的时均值为：

其中：

由图5.5.2可知：对同一流层，u′x与u′y总为异号，即正的u′y总伴随着负的u′x，为了使上面的紊流附加切应力永远为正，需在上式右端加一负号，即

在高雷诺数的紊流中，由于液体质点混掺强烈，所以动量交换也强烈。因此，式（5.5.8）中右边的第二项远大于第一项，所以紊流时的水头损失远比层流时的水头损失大。

2.紊流附加切应力与时均流速的关系

因为紊流附加切应力中的脉动流速u′x和u′y是不易确定的量，所以，我们设法建立脉动流速与时均流速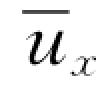 的关系。为此，普朗特（Prandtl）提出了混合长度的假说。该假说认为紊流状态下液体质点的混合长度类似于分子运动中的平均自由程。在气体中，一个分子在撞击另一个分子之前所行进的平均距离称为平均自由程。与此相类似，当液体质点从具有某一速度的液层进入具有另一速度的液层时，在液体质点相互撞击而使其具有的动量改变之前，液体质点沿垂直于时均流速 的方向移动了距离l，然后该液体质点与另一层液体具有相同的物理性质，这个横向距离l就称为混合长度，如图5.5.3所示。

图5.5.3(www.daowen.com)

两层之间的时均流速之差为：

普朗特认为：u′x与u′y是相关的，且为同一量级，这由连续原理可以说明，而u′x和u′y与两液层间的时均流速之差具有相同量级，也就是说它们彼此之间成比例，即

式中C为常数，由于l还是一个待定的数值，所以，可以将C包括在l内。于是，紊流附加切应力的式（5.5.7）可以写成为：

或者

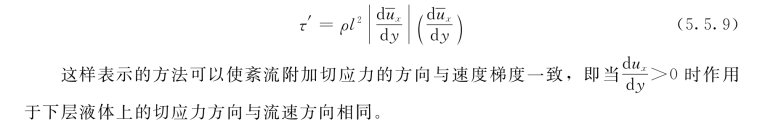
由于脉动流速u′x和u′y越靠近边壁处越小，而在边壁处u′x=u′y=0，所以普朗特假设混合长度l正比例于到边壁的距离y，即

式中к称为卡门（T.von K′arman）常数，由实验得靠近壁面处к=0.4。

式中 ε——紊动运动黏滞系数，类似层流中的运动黏度ν；

η——紊动动力黏滞系数，类似层流中的动力黏度μ。

当均采用时均值描述紊流运动，并且以u表示x 方向的流速时，可以省去时均流速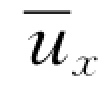 中的平均符号“-”和脚标“x”于是，紊流中的总切应力可以表示为：