我们知道，紊流中有许许多多的小漩涡，每个小漩涡都有各自的物理特征和力学特征。当流场中某个空间点处不同时刻由不同的小漩涡占据时，该空间点处的物理特征和力学特征也将随时间而变化。将紊流中某一空间点处的运动要素 （速度u、压强p）随时间而变化称为脉动现象。将流体质点在某一瞬间通过某一空间点的流速称为该空间点的瞬时流速。它可以分解成为ux、uy、uz。在图5.5.1上给出了紊流流场中某空间点处瞬时流速ux随时间t的变化的曲线。

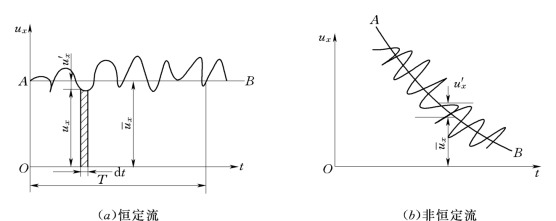
图5.5.1

由图中可以看出，该空间点处的瞬时流速ux是随时间变化的，但是，在足够长的时间过程中，对于恒定流来讲，它的时间平均值是不变化的，如图5.1.1 （a）所示，时间平均流速曲线AB是平行于t轴的一条直线。取足够长的时间为T，则在此时间T过程的时间平均流速用下式定义：

对于非恒定流，时间平均流速是指在某一时段内流速的平均值，但这一时段的流速平均值和另一时段流速的平均值一般讲是不相同的，若规定了时段的长短后，则可得其时间平均流速，这时时间平均流速曲线如图5.5.1 （b）所示。

紊流流场中某空间点处的瞬时流速与时间平均流速之差值称为脉动流速，记为u′x（或u′y、u′z），即

或者

即某点的瞬时流速等于时间平均流速与脉动流速之和。(www.daowen.com)

脉动流速的时间平均值为零。例如对于脉动流速u′x=ux-ux在时间T 过程中的时间平均值为：

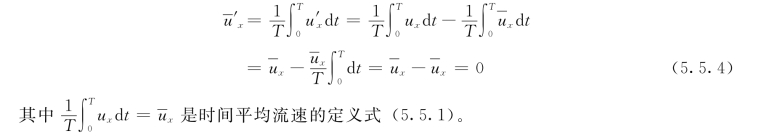
在层流中因为没有脉动流速，因此时间平均流速与瞬时流速相等。

在水力学中常用脉动流速的均方根表示脉动幅度的大小，记为σ，即

而用脉动流速的均方根与时均特征流速v之比表示紊动强度，并记为Tu，即

对于管流和明渠，以断面平均流速作为时均特征流速；对于绕流物体，以远离物体的来流速度作为时均特征流速。对于动水压强类似地有：

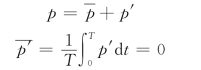
水流的脉动现象对工程的影响是：①增加能量损失，这时水头损失约与速度的平方成比例；②增加作用荷载，因为动水压强的瞬时值有时大于时均压强值；③易引起共振现象；④脉动流速可以加剧河底泥沙的运动，减小淤积；⑤使流速分布趋于均匀化等。