假设在如图5.4.1所示的圆管中发生液体的层流运动，这时，我们可以将圆管中的层流看作是许多无限薄的同心圆筒液层间的相对运动。每一层表面上的切应力由牛顿内摩擦定律确定，取管轴线方向为x，则

图5.4.1

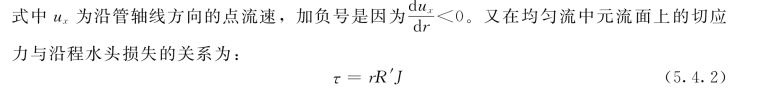
令式（5.4.1）、式 （5.4.2）相等，得：

积分得：

可见圆管层流中的流速是抛物型分布。

在r=0 （管轴心）处流速最大，即ux=uxmax，所以：

圆管层流中的断面平均流速由下式求得，即

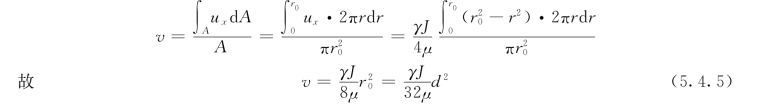
由式（5.4.4）和式（5.4.5）可知：在圆管层流中，断面平均流速是断面上最大流速的1/2，即

由式（5.4.5）得：

(www.daowen.com)

式 （5.4.7）表明：圆管层流中的沿程水头损失与断面平均流速的一次方成比例，这与由雷诺实验得到的结论相同。

由达西—威斯巴赫公式（5.2.9）与上面式（5.4.7）式中的沿程水头损失可得：

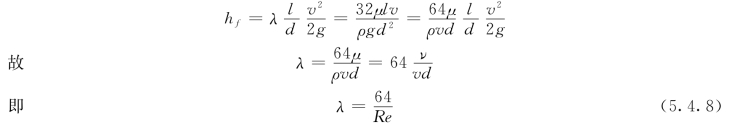
式 （5.4.8）表明：圆管层流中的沿程水头损失系数只与雷诺数有关且成反比例关系。

例5.4.1 动力黏度为3.5×10-2N·s/m2，密度为830kg/m3的油，以流量为3×10-3m3/s在内径为5cm的圆管中流动。试求：

（1）该流动是层流还是紊流。

（2）管长50cm上的水头损失。

（3）距离壁1.5cm处的点流速。

解：

（1）判断该流动是层流还是紊流

此流动的雷诺数为：

（2）水头损失hf计算

（3）距管壁1.5cm处的点流速计算

由式（5.4.3）：