人们从实践中早已观察到实际液体运动时有两种不同的型态。但是，直到1883年英国的雷诺（O.Reynolds）才通过实验揭示出这两种不同流动型态的本质。

如图5.3.1所示为雷诺实验装置。上游是一个保持恒定水位的水箱D，由侧壁引出一根进口为喇叭形的平直的玻璃管T，为了量测水头损失，在其上装两根测压管，为了调节管中的流速，在管路的末端装有阀门K，下游设有接水容器C。为了显示水流的运动型态，在上游水箱顶部放一盛红颜色水的容器C1，在其下用针形细管引入到玻璃管的喇叭形进口处，针形管的上端装一阀门P。

试验时先将阀门K微微打开，液体从玻璃管中流出，然后将阀门P打开，红颜色水流入玻璃管T中。这时在玻璃管中有一条平直的红颜色线束，此线并不与周围水体混掺，如图5.3.2 （a）所示。再将阀门K逐渐开大，玻璃管中的流速就逐渐增大，这时就可以看到红颜色的流束开始颤动并弯曲，有波状外形，如图5.3.2 （b）所示。以后流束开始破裂，失去清晰的形状。最后当流速达到一定值时，带红颜色的流束完全破裂，形成许许多多的小漩涡充满整个玻璃管，如图5.3.2 （c）所示。它说明此时流体质点间互相混掺。

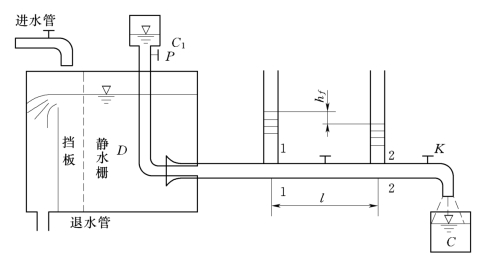
图5.3.1

上面实验说明：同一种液体在同一管道中流动，当流速不同时液体有两种不同的运动型态。

（1）当流速较小时，各液层的质点互不混掺，作有条不紊的直线运动，此种流动型态称为层流。

（2）当流速较大时，管中形成涡体，各液层质点互相混掺，作杂乱无章的运动，此种流动型态称为紊流。

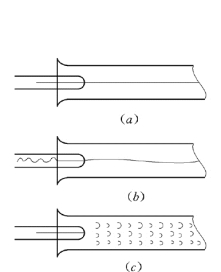
图5.3.2

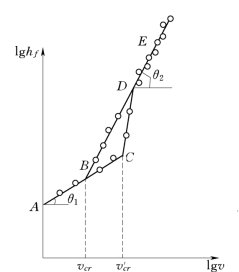
图5.3.3(www.daowen.com)

当实验以相反的程序进行时，则流动从紊流转变成层流。但是，由紊流转变为层流时的流速比由层流转变为紊流时的流速小。

雷诺又在上面的实验设备上量测了沿程水头损失hf与管中断面平均流速v之间的变化关系。通过两测压管中的水位差可得到水头损失hf。写1-1断面、2-2断面的能量方程式，以管轴线为基准，得：

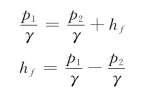
即两根测压管中得水位差就是1-1断面和2-2断面间的水头损失。通过容器C量测流量Q，进而可计算管中的断面平均流速v。

假如以lg v为横坐标轴，以lg hf为纵坐标轴，将测得的数据绘出，如图5.3.3所示。将液体流动型态转变时的流速称为临界流速。当实验流速由小变大时，变化曲线为ABCDE，层流维持到C点，以后转变为紊流。C点所对应的流速称为上临界流速，记为v′cr。当实验流速由大变小时，变化曲线为EDBA，紊流维持到B点，以后转变为层流。B点所对应的流速称为下临界流速，记为vcr。B、C点之间称为过渡区，可能是层流也可能是紊流，依实验程序而定。线段AC和DE 都是直线，可以用下面的方程式表示：

式中 lg k——截距；

m——直线的斜率。

上式的指数形式为：

由实验得到：AB直线与水平轴夹角θ1=45°，即m=1，所以层流时沿程水头损失与速度的一次方成比例。DE线与水平轴夹角θ2＞45°，约为60°15′～63°26′，即m=1.75～2.0，所以紊流时的沿程水头损失与速度的1.75～2.0次方成比例。