由于实际液体在运动时存在有切应力，故液体在运动过程中摩擦生热并将其耗散在水流中，对于机械能而言，这部分热能是不可逆的，因此水流中产生机械能损失，也就是水头损失。可见沿程水头损失hf是直接与水流同固体壁面接触处的切应力τ0有关系的。下面将先建立均匀流中的沿程水头损失hf与切应力τ0之间的关系。

现在，从图5.2.1所示圆管总流中取出长度为s的一段作为控制体，研究其平衡。假设流动是恒定的均匀流，且液体是不可压缩的。

图5.2.1

由于该流动是恒定流，所以没有时间加速度，又由于是均匀流，所以也没有位移加速度，故该流动液体的全部加速度为零。我们用牛顿第二定律∑Fs=mas研究上述控制体的平衡。由于全加速度as=0，所以∑Fs=0。脚标s表示沿管轴方向。

设过水断面1-1和2-2形心的位置高度分别为z1、z2，作用的压强分别为p1、p2，管轴线与水平面间的夹角为α，水的容重为γ，过水断面面积为A，湿周为X，则作用在控制体上的表面力，其一是作用在两端过水断面上的动水总压力，即

其二是作用在控制体侧面上的摩擦力，即

作用在控制体上的质量力在s方向上的分量为：

根据∑Fs=0，得：

两端除以γA，得：

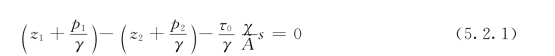
写1-1和2-2断面的能量方程式，得：

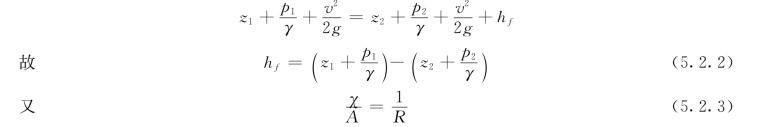
将式（5.2.2）、式 （5.2.3）代入式（5.2.1），得：

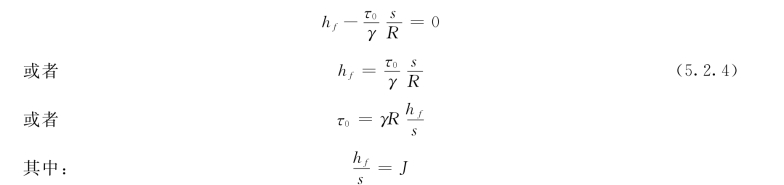
式中 J——水力坡降。所以：

对于水力半径为R′的同心圆筒式元流，其元流表面的切应力τ为：

(www.daowen.com)

由式（5.2.5）和式（5.2.6），得：

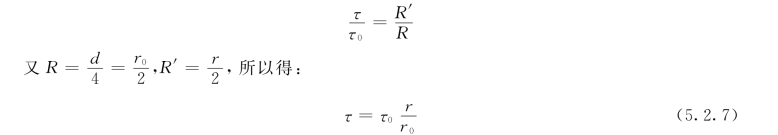
式 （5.2.7）说明圆管均匀流过水断面上的切应力按直线规律分布，管壁处最大为τ0，管轴线处最小为零，如图5.2.2所示。

图5.2.2

式中 l——管段长度；

λ——沿程水头损失系数，它与液流型态等有关。

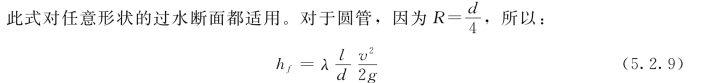
式 （5.2.9）称为达西—威斯巴赫（Darcy-Weisbach）公式。

例5.2.1 水流在直径d=30cm的圆管中流动时，在l=100m管长上测得水头损失hf=2m。试求：

（1）管壁上的切应力τ0。

（2）当沿程水头损失系数λ=0.025时的断面平均流速v。

解：

（1）τ0计算

由式（5.2.5）

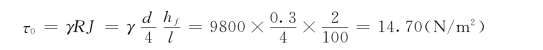
（2）断面平均流速计算

由式 （4.4.9）

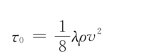
得：