利用量纲和谐原理可以分析液流物理量之间的关系并在一定程度上导得描述水流运动的物理方程式。这种方法称为量纲分析法。它是解决水力学问题的有效途径之一。

量纲分析的方法有许多，下面主要介绍两种方法：①瑞利 （Rayleigh）方法；②布金汉（E.Buckingham）π定理。前者适用于涉及的物理量较少的情况，后者的适用性则更广泛些。

1.瑞利方法

瑞利方法是直接用量纲和谐原理建立物理量间的函数式。下面通过例题来说明。

例4.4.1 试用瑞利方法推导圆形孔口出流的流速表达式。

解：

根据对孔口出流现象的观察分析，可以认为通过孔口的流速与下列因素有关：孔口的作用水头H，重力加速度g，水的密度ρ及动力黏度μ，即v=f（H，g，ρ，μ）。瑞利方法首先将上式表示为幂指数乘积的形式，即

式中 k——无量纲常数；

a、b、c、d——待定指数。

然后将式中各物理量的量纲都用基本量纲M、L、T表示，得：

根据量纲和谐原理，得出下列关系：

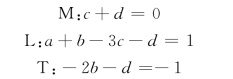
上面有三个方程式，其中包含有四个未知数，现将其中d作为待定值，于是得：

代入式（4.4.3）后有：

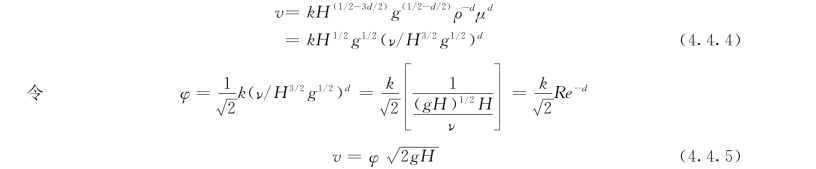
式中 φ——流速系数，可由水力学试验确定其数值。

例4.4.2 如图4.4.1所示圆管中水流，试用瑞利方法推导沿圆管壁面切应力τ0的表达式。

图4.4.1

解：

通过观察分析可以认为圆管壁面上的切应力τ0与下列物理量有关：圆管的直径D、管中断面平均流速v、液体的密度ρ、动力黏度μ及用平均突出高度Δ 表示的管壁的粗糙度。它们之间的关系可用函数表达如下：

应用瑞利方法时首先将上述函数关系表达为幂指数的乘积形式，即

式中 k——待定常数；

a、b、c、d、e——待定指数。

将式（4.4.6）中各物理量的量纲用基本量纲M、L、T表达，得：

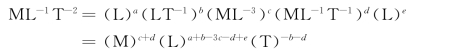
根据量纲和谐原理，等式两边同类基本量纲的指数应该相同，即

现以b、e为待定系数，将式（4.4.7）中a、c、d用b、e表示，则

将式（4.4.8）代入式（4.4.6），得：

注意到：

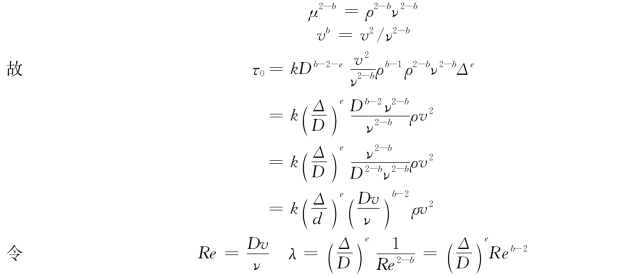
式中 λ——圆管沿程水头损失系数。

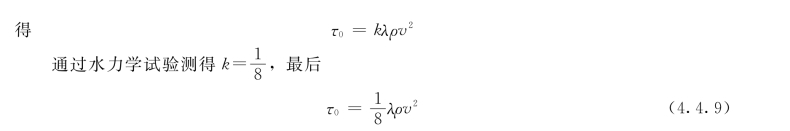
由上面两个例题可以看出，由于基本量纲只有三个，当影响流动的因素也是三个时，应用瑞利方法十分方便。若影响流动因素多于三个时，不得不选取待定的指数。所以瑞利方法只适用于涉及的物理量较少的情况。

2.布金汉π定理

π定理指出：任何一个物理过程，如果存在n个物理量互为函数关系：

如这些物理量中有m 个基本量，则这个过程可排列成 （n-m）个无量纲数π1，π2，…，πn-m的函数关系式：

函数式中的无量纲数π1，π2，…πn-m可按以下步骤得出。

（1）确定与所研究对象有关的n个物理量，如A1，A2，…，An。这一步是分析结果正确与否的关键，这要靠研究者对所研究对象的深刻认识与全面理解。在水流运动中涉及的物理量应包括水的物理特性，运动特性及边界的几何特性。

（2）从n个物理量中选取m 个基本物理量，m一般为3，如A1、A2、A3。这三个基本物理量在量纲上应是独立的，即是指其中任何一个物理量的量纲不能从其他两个物理量的量纲中诱导出来。如果用

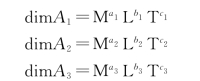
来表示基本物理量的量纲式，则A1、A2、A3不能形成无量纲量的条件是量纲式中的指数行列式不等于零，即

由式（4.4.11）可验证A1、A2、A3是否为基本物理量。

（3）确定无量纲量的个数k=n-m。

（4）从m个基本物理量以外的（n-m）个物理量中每次轮取一个，与基本物理量组成一个无量纲的π数，共写出（n-m）个，即

(www.daowen.com)

（5）将上述各项右端的各物理量用基本量纲 （M，L，T）表示，因为π是无量纲数，故其量纲dimπ=M 0L0T0=1，这样，根据量纲和谐原理就可求出各π项的指数ai、bi、ci（i=1，2，…，n-m）。即式 （4.4.12）中第一式物理A4的量纲应与Aa11Ab12Ac13的量纲一样，其他各式依此类推。

（6）组成无量纲表达式：

下面通过例题来说明这一过程。

例4.4.3 试用布金汉π定理推求船体以速度v在水中行进时的阻力表达式。

解：

计算步骤如下。

1）根据观察和分析，确定与本问题有关的物理量。与阻力F有关的物理量有船体的吃水深度h、船的运动速度v、重力加速度g、水的密度ρ及动力黏度μ，写成下述函数式：

2）选取基本物理量为h、v、ρ。根据三个基本物理量的量纲公式：

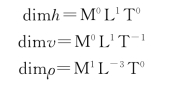
各指数的行列式不为零：

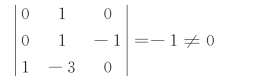
所以上列三个基本物理量的量纲是独立的。

3）无量纲量的个数为6-3=3。

4）将h、v、ρ以外的三个物理量F、g、μ分别与h、v、ρ组成π项：

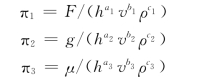
5）由量纲和谐原理求出ai、bi、ci。

由式（4.4.14）解得：a1=+2，b1=+2，c1=+1。于是：

由式（4.4.15）解得：a2=-1，b2=+2，c2=0。于是：

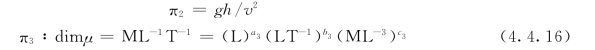
由式（4.4.16）解得：a3=+1，b3=+1，c3=+1。于是：

6）组成无量纲表达式：

式 （4.4.17）可以写成：

由于h 2具有面积的量纲，故式（4.4.18）写成：

其中：

式中 CD——绕流阻力系数。

由水力学试验可求出各具体情况的CD值。

例4.4.4 试应用布金汉π定理求出水平等直径有压圆管中液体流动压强降落的表达式。

解：

计算步骤如下：

1）经观察分析可知有压管内液体流动压强降落Δp与以下因素有关：管径d、管长l、管壁粗糙高度Δ、流体速度v、液体的密度ρ及液体的动力黏度μ。写出函数表达式为：

2）选取基本物理量为d、v、ρ，这三个基本物理量的量纲公式：

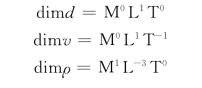
各指数行列式不为零：

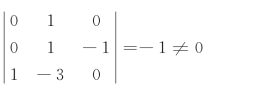
3）无量纲量的个数为7-3=4。

4）将d、v、ρ以外的4个物理量Δp、l、Δ、μ分别与d、v、ρ组成4个π∶π1、π2、π3、π4。

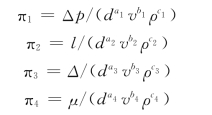
5）由量纲和谐原理求得：

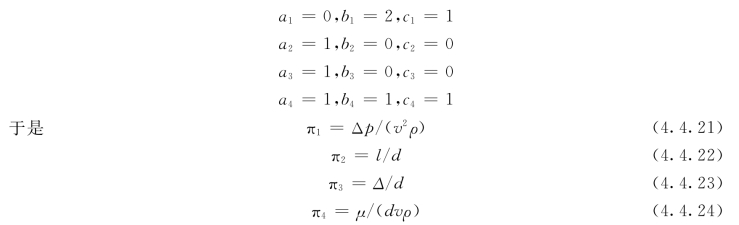
6）组成无量纲表达式：

由式（4.4.26）写出压差表达式为：

压强的降落与管长成正比与管径成反比，于是：

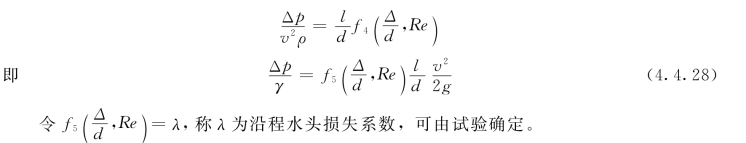
由上述可见，量纲分析作为一种工具已被广泛地应用到水力学和模型试验等领域。然而量纲分析毕竟是一种数学分析方法，正确利用它的前提是要求人们正确理解流动的物理现象和影响因素。尤其是最后确定物理公式具体形式时，还要靠理论分析和试验的成果。