控制体形式的动量矩方程的一般式为：

对于恒定流，上式右端的非恒定项为零，于是得：

式 （3.8.12）就是恒定流时对控制体而言的向量形式的动量矩方程。它说明：恒定流时，作用在控制体上的外力关于某轴的外力矩的向量和等于单位时间内通过控制体表面流出与流入的动量矩之差。

例3.8.4 图3.8.6 （a）所示为水泵叶轮的平面图，①为进口断面，②为出口断面，进出口断面到转轴O的距离分别为r1和r2；vr和vt分别表示绝对速度v在径向和切向的速度分量。试用动量矩方程推导水泵扬程水头的表达式：

式中 u1、u2——叶轮进出口处的牵连速度或者圆周速度；

v1、v2——叶轮进出口处的绝对速度；

α1、α2——叶轮进出口处的绝对速度与圆周速度间的夹角。

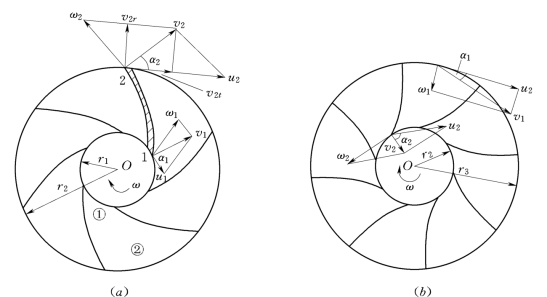
图3.8.6

解：

由于叶轮中水流的流动是恒定的，所以应用动量矩方程（3.8.12），即

注意：式 （3.8.12）中的速度u相当于图3.8.6中叶轮进出口处的绝对速度v （v1或v2），所以：

将此代入式（3.8.12），得：

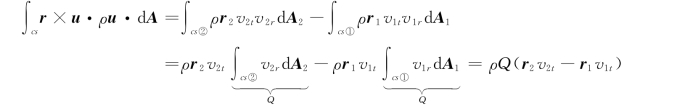
由图中可知，式中v2t=v2cosα2，v1t=v1cosα1，令Tqcv=T，所以得：

从机械方面而言，水泵的功率为：

式中 ω——叶轮的旋转角速度。

又r2ω=u2，r1ω=u1，u1、u2为叶轮进出口处的圆周速度，所以：

从水力学角度而言，水泵的功率为：

(www.daowen.com)

令式（3.8.14）等于式（3.8.15），则最后得：

又离心泵进口叶片的安置角常为α1=90°，即cosα1=0，注意到v2cosα2=v2t，所以得：

对于图3.8.6 （b）所示的水轮机叶轮，由于液体是从叶轮的外缘流向内缘，即水泵叶轮的进口断面恰为水轮机叶轮的出口断面，水泵叶轮的出口断面恰为水轮机叶轮的进口断面，若水流流进断面为1-1断面，水流流出断面为2-2断面，当假设水轮机的水头为Ht时，用与上述完全相同的推导方法，则可以得到水轮机的水头公式为：

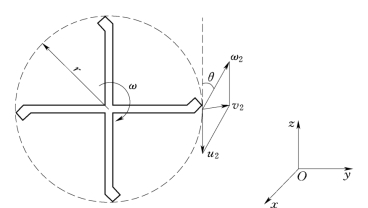
图3.8.7

例3.8.5 有一如图3.8.7所示的对称臂的洒水器平面图，已知：轴向总供给流量Q=2.5L/s，然后通过4个旋转臂射出，各臂的内径均为d=1cm，半臂长r=0.5m，射流的方向角θ=30°如图中所示，试求：

（1）使洒水器固定不动时所需加的外力矩T。

（2）忽略转轴的摩擦力时洒水器的转数n。

解：

（1）计算施加外力矩T

设洒水器出口水流运动的速度三角形如图所示，其中u2、ω2及v2分别为圆周速度、相对速度及绝对速度。当洒水器不动时，即ω=0，圆周速度u2=ωr=0，这时v2=ω2，且方向相同。

根据动量矩定律有：

但是，由于水流是沿半径方向流入，故在x Oy平面内v1t=0，v2t=ω2cosθ，所以得：

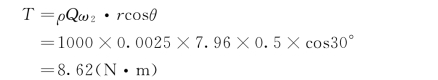
（2）计算转数n

当洒水器旋转时，圆周速度u2不为零，但是外力矩T为0，又这时式 （3.8.19）中的ρQv1t·r1=0，同时由出口速度三角形可知：

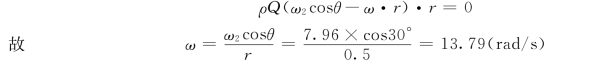
所以由式（3.8.19）得：

最后得转数为：