在工程实际中，常遇到求流动的水流对固体边界的作用力问题，例如求图3.8.1 （a）中所示的水流作用在闸门上的作用力R′x，图3.8.1 （b）中所示的水流作用在弯管上的作用力R′x和R′z等。此类问题用动量方程求解比较方便。

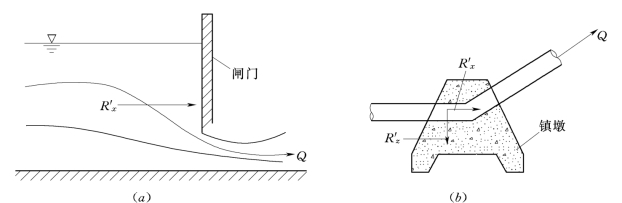
图3.8.1

控制体形式的动量方程的一般形式为：

对于恒定流，上式右端的非恒定项为零，于是得：

式 （3.8.2）说明：对于恒定流，作用在控制体上外力的向量和等于单位时间内通过控制体表面流出与流入控制体的动量之差。

现在对于图3.8.2所示的恒定总流应用式 （3.8.2）。从总流中取出一元流。元流在1-1断面和2-2过水断面处的断面面积分别为d A1和d A2，流速分别为u1和u2。该元流单位时间流出与流入的动量差为：

对于该总流单位时间内流出与流入的动量差为：

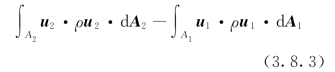
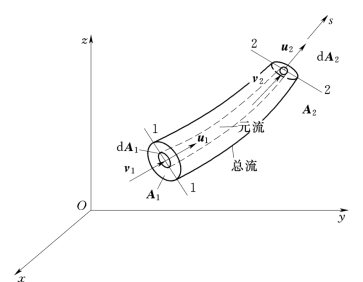
图3.8.2

式中的u2和u1用相应过水断面的断面平均流速v2和v1代替，但两者计算的动量有差异，为此需要修正。设1-1断面与2-2断面为均匀流或渐变流断面，u与v的方向几乎相同，则可引入动量校正系数α0，它表示实际动量与按v计算的动量之比，即

α0值与断面上的流速分布有关，约为1.02～1.05，为了简化可取α0=1。

将式（3.8.4）代入式（3.8.3），并注意到ρ等于常数和v1A1=v2A2=Q，得：

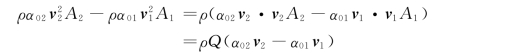
因为动量是向量，所以上式中保留了v2和v1。

最后，得恒定总流动量方程的向量形式为：

其分量形式为：

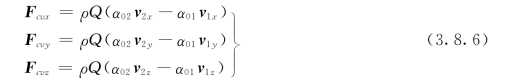
应用动量方程注意的事项：

（1）在渐变流断面间取控制体，便于用能量方程求压强p。

（2）原则上压强标准可以采用相对压强或绝对压强，但多数情况下采用相对压强更方便些。

（3）视其方便选取坐标轴方向，注意作用力及速度的正负号。

（4）外力F应该包括作用在控制体上的所有质量力、表面力 （主要指压力）和固体边界的反作用力。固体边界的反作用力的方向可以事先假设。解出为正时说明假设的反作用力方向与实际相符合，否则实际的反作用力方向与假设方向相反。

（5）应为流出控制体的动量减去流入控制体的动量。

（6）当问题中所需要的流速和压强均未知时，需要与连续方程和能量方程联解。

例3.8.1 有一如图3.8.3所示的溢流坝，当通过的流量Q为50m3/s时，坝上游水深H=10m，坝下游收缩断面的水深hc=0.5m，已知坝长 （垂直于纸面方向）L=10m，试求水流对坝体的总作用力。

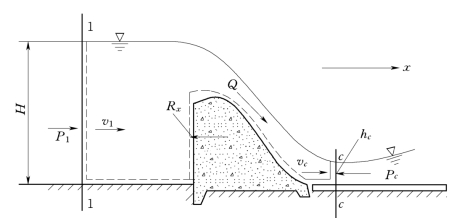
图3.8.3

解：

取水平向右方向为x轴正向，水流对坝体只有x方向的作用力。取图中虚线和自由水面线所围水体为控制体，在x方向上作用在控制体上的作用力，当忽略空气和床面与水体的摩擦力时，只有作用在1-1和c c断面上的动水压力P1和Pc，以及坝对水体的反作用力Rx。于是，对该控制体x方向的动量方程为：

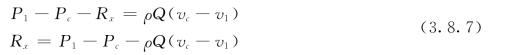
我们认为1-1和c c断面处水流符合渐变流条件，因此，动水压强按静水压强规律分布，即

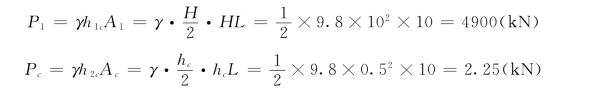
由连续方程求1-1断面和c c断面的平均流速分别为：

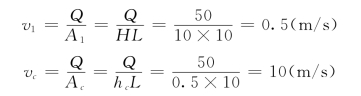
将上面各值代入式 （3.8.7），因为动水压力是以k N 为单位，所以式中ρ虽然为1000kg/m3，但只代入数值1，于是得：

所求得的Rx为正值，说明我们假设的方向正确。那么，根据作用力与反作用力大小相等方向相反，则水流作用在坝体上的作用力R′x为4412.75k N，但方向沿x轴正向。

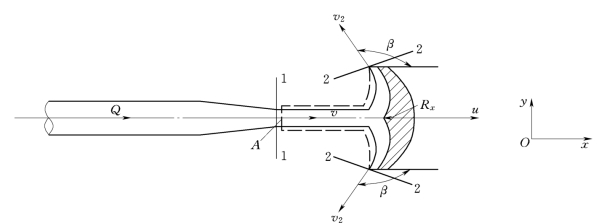
例3.8.2 如图3.8.4所示喷嘴射流冲击弯曲叶片。已知射流流量为Q，喷嘴出口流速为v，叶片出口的流速与水平方向的夹角为β，试求：

(www.daowen.com)

图3.8.4

（1）射流对弯曲叶片的作用力。

（2）射流对平板叶片的作用力。

（3）当叶片以速度u向右移动时，射流对弯曲叶片的作用力。

解：

（1）弯曲叶片时

取1-1断面和2-2断面水体为控制体。如图3.8.4所示取x轴和y轴。因为射流各处的位置z相同，且均在大气压力作用下，若不计水头损失，由能量方程式得v=v2。又由于叶片对称，所以y方向的作用力总和为0。

设叶片对控制体的作用力为Rx，x方向的动量方程为：

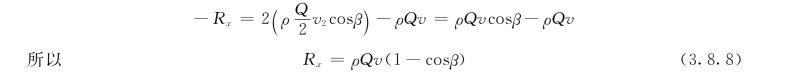
当β=180°时cosβ=-1，所以作用在弯曲叶片上的最大作用力为：

（2）平板叶片时

这时β=90°，cosβ=0，所以由式（3.8.8）得：

可见曲面叶片所受的最大作用力为平板所受作用力的2倍，这就是叶片机械做成曲面的原因。

（3）当弯曲叶片以速度u向右移动时

这时式 （3.8.8）中的速度v应该用相对于叶片的速度v u代替，流量Q用 （v-u）A代替。这相当于用相对于叶片的流速和流量。于是：

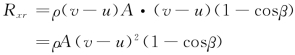
例3.8.3 在立体图上有一如图3.8.5所示的弯管段。已知：弯管段入口和出口的直径分别为0.5m和0.25m；折角θ=60°；管中通过的流量Q=0.4m3/s；弯管入口处的相对压强p1=147k N/m2；弯管段的水重G=5k N，进出口断面的高程差Δz=2m。试求水流对弯管的作用力。

解：

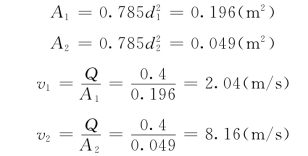
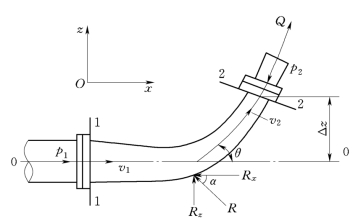
图3.8.5

以图中0-0为基准面，写进出口断面的能量方程，则

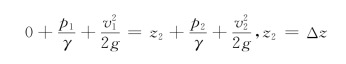
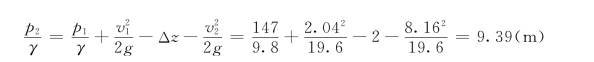
所以

1-1断面和2-2断面上作用的动水总压力分别为：

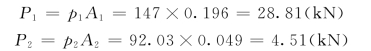
现在，按图示坐标系统，取1-1断面和2-2断面间的水体为控制体。作用在控制体上的外力有：1-1断面和2-2断面上的动水总压力、水体的重量和弯管对水体的反作用力。设弯管对水体的反作用力的x和z方向的分量分别为Rx和Rz。

x方向的动量方程为：

所以

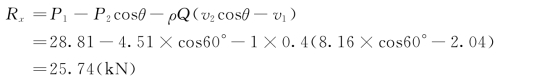
z方向的动量方程为：

所以

因为求得的Rx和Rz均为正值，所以假设的反作用力的方向正确。反作用力的合力大小为：

合力与水平方向的夹角为：

最后，水流对弯管的作用力大小为28.29k N，方向与R方向相反。