假设我们研究的液体是重力作用下的不可压缩的理想液体。下面我们应用控制体形式的动量方程（3.3.16）来推导元流的能量方程。

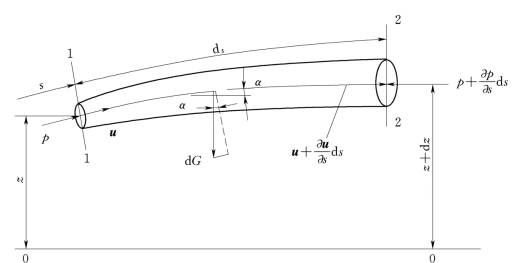
图3.5.1

当忽略二阶微量后可以近似地认为整个控制体内液体的流速为us=u，体积V=d s d A，于是式（3.5.2）右端的非恒定项就可写为：

式 （3.5.2）右端的第二项通量项，对于所取控制体可以写为：

而其中：

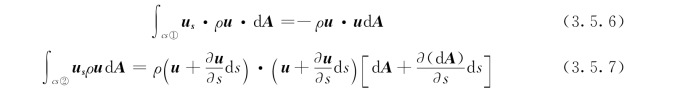
由连续方程可知：

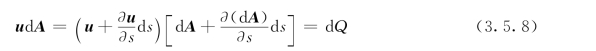
将式（3.5.6）、式 （3.5.7）和式（3.5.8）代入式（3.5.5），得：

(www.daowen.com)

最后，将式（3.5.3）、式 （3.5.4）和式（3.5.9）代入式（3.5.2），得：

或者写为：

将上式的两端除以该段元流的重量γd s d A，得：

此式是微分形式的能量方程，它在第11章非恒定流动中将有重要的应用。

对式（3.5.10）沿s轴从s1积分到s2，得：

式 （3.5.11）是理想不可压缩液体在重力作用下非恒定元流的能量方程。

对于恒定流，hi=0，于是式（3.5.11）变为：

式 （3.5.12）也称为伯努利方程，因为它是瑞士科学家伯努利 （D.I.Bernoulli）于1738年推导出来的。它表明：恒定流时，对于理想液体，在元流的任意两个过水断面1 1和2-2上，单位重量液体所具有的总机械能（位能、压能、动能之和）是相等的。