质量守恒定律在水力学中的具体表现形式为连续方程。其一般形式为式（3.3.15），即

对于不可压缩液体的非恒定流，ρ=常数，则得：

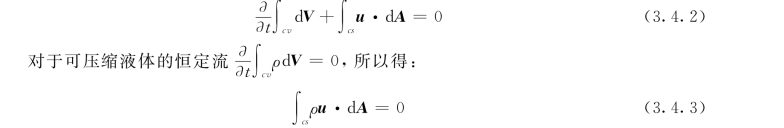
对于不可压缩液体的恒定流，式 （3.4.3）变为：

式 （3.4.3）和式（3.4.4）说明：在恒定流时流出与流入控制体表面的质量流量（可压缩液体）或体积流量（不可压缩液体）之差为0。

例3.4.1 有一如图3.4.1所示的管道中的恒定水流运动，设断面1-1、2-2的过水断面面积分别为A1、A2，其断面平均流速分别为v1、v2，试建立该总流的连续方程。

解：

取图中1-1、2-2断面与管壁所围空间ABCD 为控制体，由于流动是恒定的，所以连续方程为式（3.4.3），即

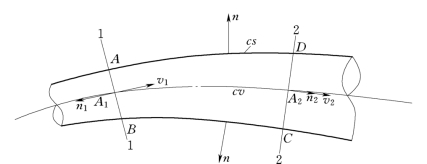
图3.4.1

式中 u1、u2——过水断面1-1、2-2上各点的流速。

设v1和v2为各断面的断面平均流速，则由式（3.1.3）得：

式 （3.4.5）说明：在恒定流中单位时间内通过各个断面的质量相等。对不可压缩性液体ρ1=ρ2=ρ，于是得：

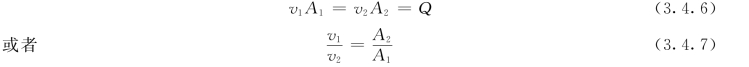
式 （3.4.6）及式（3.4.7）说明了在恒定流中，当液体不可压缩时，各断面通过的流量相同，并且断面平均流速与过水断面面积成反比。

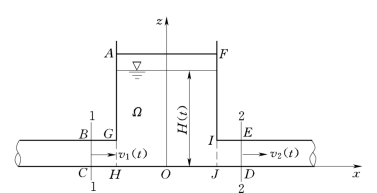
图3.4.2

例3.4.2 如图3.4.2所示为一隧洞中的调压井。设进水及出水隧洞的过水断面面积分别为A1、A2，断面平均流速分别为v1、v2，调压井的横断面积为Ω。试建立调压井中水位随时间的变化规律。

解：

当进水隧洞和出水隧洞的流量不相等，即v1A1≠v2A2时，调压井中的水位将随时间变化，此问题属于不可压缩液体的非恒定流问题，取如图3.4.2中ABCDEF空间为控制体，并应用非恒定流的连续方程（3.4.2），即

设在时刻t时调压井中的水位为H（t），则

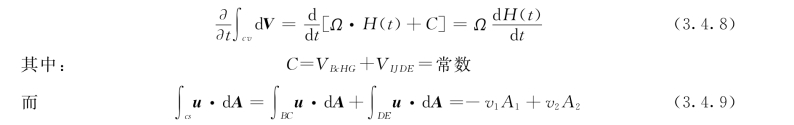
现将式（3.4.8）、式 （3.4.9）代入式（3.4.2），得：

(www.daowen.com)

或者

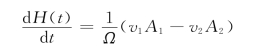
上式表达了调压井中的水深变化率与进、出隧洞的流量之间的关系。

例3.4.3 试推导有压管路非恒定流和明渠非恒定流的连续方程。

解：

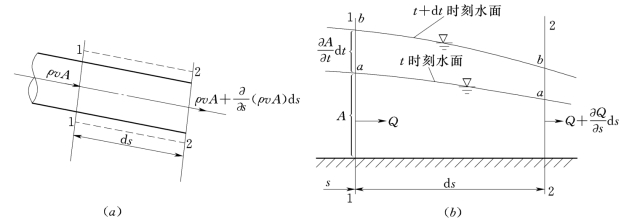
图3.4.3

由前述可知：

将式（3.4.10）、式 （3.4.11）代入式（3.4.1），并注意到式（3.4.10）中的d s不随时间变化，则得有压管路非恒定流的连续方程为：

对于图3.4.3 （b）所示的明渠非恒定流，如果取1-1、2-2断面间空间为控制体，仿照有压管路非恒定流，可以导出连续方程。但是，注意到明渠非恒定流中的液体可作为不可压缩处理的特点，即ρ=常数，可直接由式 （3.4.12）导得连续方程。在式（3.4.12）中令ρ=常数，并注意到v A=Q，则得明渠非恒定流连续方程为：

例3.4.4 有一如图3.4.4所示的压缩空气罐。已知罐内的容积V=0.05m3，压缩空气的密度ρ=6kg/m3，当罐的出口阀门突然打开时，喷出气体的瞬时速度u=300m/s，出口断面积A=70mm2。试求：开启阀门瞬间罐内气体的密度随时间的变化率。（设罐内气体的密度均匀分布。）

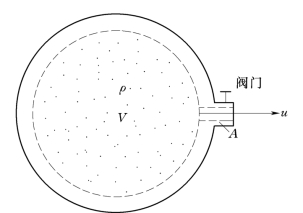
图3.4.4

解：

因为罐内气体的质量（或密度）随时间变化，故此问题属于非恒定流向题。取图中虚线所围成空间为控制体。对控制体应用非恒定流时的连续方程式（3.4.1）即

因为假设罐内的气体在任何时刻都是均匀分布的，故可以将上式中的密度ρ提到积分号外面，这时，第1项变为：

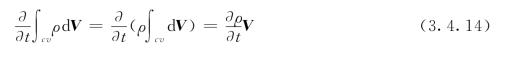
而第2项变为：

将式（3.4.14）、式 （3.4.15）代入式（3.4.1），得：

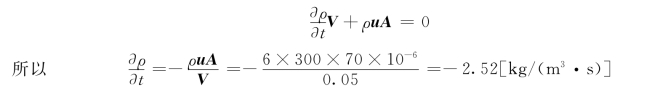
式中负号表示罐中气体的密度随时间增加而减小。