在如图3.3.2所示的坐标系中，在t时刻有一质点系s0，在t+δt时刻该质点系运动到新的位置s。s0就相当于图3.3.1中的ABCD，s相当于abcd。现在我们分别针对质点系和控制体建立质量守恒定律、动量定律及动量矩定律。

1.质量守恒定律

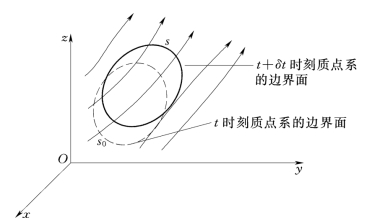
图3.3.2

若将t+δt时的质点系s同t时的质点系s0相比较，它们的位置不同，形状也可能不同，但是由于质点系的边界是封闭的，没有液体流进或流出，所以s和s0内的质量是相同的，即质点系内没有质量变化，或者说质点系中的质量对时间的导数等于零，即

符号 “sy”表示系统。而质点系中的质量为：

式中 ρ——液体的密度；

V——质点系的体积。

2.动量定律

作用在质点系上的所有外力的向量和，等于质点系所具有的动量对时间的导数，即

式中 Fsy——作用在质点系上外力的向量和，包括质量力和表面力。

质点系的动量可以表示为：

(www.daowen.com)

3.动量矩定律

作用在质点系上的外力关于某轴力矩的向量和，等于该质点系关于同一轴的动量矩对时间的导数，即

式中 Tqsy——作用在质点系上的外力关于某轴的力矩向量和，包括质量力力矩和表面力力矩。

质点系关于同一轴的动量矩可以表示为：

式中 r——对某轴的矢径。

现将式（3.3.1）、式 （3.3.3）及式（3.3.5）右端的导数统一写成为：

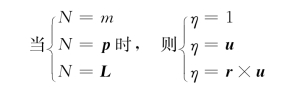
Nsy为质点系所具有的某一物理量，如质量m、动量P及动量矩L，并且可以将它表示成为：

式中 η——质点系中局部地区单位质量液体所具有的相应于N 的物理量。

式（3.3.7）称为物质的体积分。参考式 （3.3.2）、式 （3.3.4）及式 （3.3.6）可以得到下面的对应关系：