在3.2节中介绍了描述液体运动的两种方法。其中拉格朗日法是以个别的液体运动质点为对象，研究这些给定的液体质点在整个运动过程中的轨迹和运动要素随时间的变化规律。而欧拉法则是以流场中的空间点为对象，研究各时刻流场中诸空间点上不同液体质点的运动要素的分布和变化的规律。在应用这两种基本方法研究水流的运动时，研究的对象常须扩大。质点扩大为有限的液体团，空间点扩大为有限体积的空间。

应该指出，液流是物质的一种运动状态，除了有运动学方面的问题外，还有动力学方面的问题，也就是说必须考虑作用在液体上的各种力、液体与周围物体之间的相互作用以及液体运动所应遵循的某些普遍规律。例如质量守恒原理、牛顿第二运动定律、能最守恒原理等。根据液体受力及与其他物体相互作用的情况，应用这些普遍规律就能够建立起液体流动参数之间的关系式，这就是液体动力学的基本方程，然后求解这些基本方程就能够得出液体的参数及液体运动的具体行为。但是，在讲到液体受力和与其他物体的相互作用时就会涉及几何尺度问题，也就是说只有针对有一定几何尺度的液体团受力和运动时才有意义。而且液体运动所遵循的某些普遍规律的建立也要针对具有一定质量的液体团而言。液体团的几何尺度可大可小，小到质量为d m的任意小的液体质点，大到有限几何尺度的质点集合或称质点系。所以跟踪有一定几何尺度和具有相应质量的液体团，分析其受力情况，建立有关的方程式，研究其运动状况，这就是拉格朗日法的基本途径。但是，由于液体团在运动中不断地变形，跟踪液体团的行为非常困难，所以取有一定几何尺度的固定空间，该空间称为控制体。研究流经这一固定空间液体的受力情况和运动情况，建立有关液体运动的基本方程，从而研究液体流经这一固定空间的行为，这是欧拉法的基本途径。控制体的选取是人为的，根据研究问题的需要而选取形状和大小。

根据上述，有必要对质点系和控制体作进一步的描述，并且还要阐明如何将针对质点系所建立的有关液体运动的基本方程转变成针对控制体的方程。

包含着确定不变的连续的液体质点的液体团称为质点系，或称为系统，上述定义的质点系的边界有如下特点。

（1）质点系的边界随着液体一起运动，边界面的形状和大小可以随时间变化。

（2）质点系的边界处没有质量交换，即没有液体流进或流出边界。

（3）质点系的边界上受到外界作用的表面力。

（4）质点系的边界上可以有能量交换，即有能量（热或功）流入或流出边界。

被液体流过的，相对某个坐标系来说固定不变的任何几何形状的空间称为控制体。控制体的边界面称为控制面，它应是封闭的表面。占据控制体的各液体质点是随时间而改变的。(www.daowen.com)

根据上述定义，控制面有以下特点。

（1）控制面相对于坐标系是固定不变的。

（2）控制面上可以有液体的质量交换，即有液体流进或流出控制面。

（3）控制面上受到控制体以外物体加在控制体内液体上的力。

（4）在控制面上可以有能量交换，即可以有热或功流入或流出控制面。

控制体可以取有限体积，如图3.3.1 （a）所示管中ABCD 体积，也可以取图3.3.1（b）所示的微元六面体。ABCD 是固定空间，如果取位于此空间的液体为质点系，则经过某时段后，此质点系将位于图中的abcd的位置。

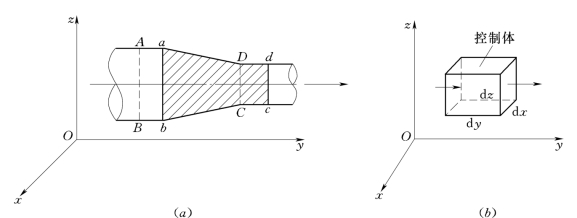
图3.3.1