与拉格朗日法不同，欧拉法的着眼点不是单个的液体质点，而是液体运动所通过的空间点。水力学中将运动液体质点所充满的空间称为流场。那么欧拉法就是考察流场中不同空间点上液体质点的运动规律，进而获得整个流场的运动规律。这里包含了两个内容：①分析流场中某个固定空间点处液体质点的运动要素随时间的变化规律；②分析流场中由于空间点发生变化所引起的液体质点运动要素的变化。可见欧拉法不是考虑单个液体质点的运动情况，而是着眼于整个流场，因此欧拉法又称为流场法。

用欧拉法研究液体运动时，流场中各运动要素是位置坐标 （x，y，z）和时间t的函数，流场中任一点的速度分量可以表示为：

式中（x，y，z）是流场中空间点的坐标，称为欧拉参数。如果令式 （3.2.5）中x、y、z为常数，则可以得到某一空间点处不同液体质点在不同时刻通过该点的流速变化规律；若令t为常数时，则可以得到同一时刻不同空间点处的流速分布。

流场中任一点处的加速度分量为：

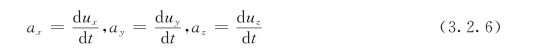
ux的全微分为：

方程两端同除以d t，得：

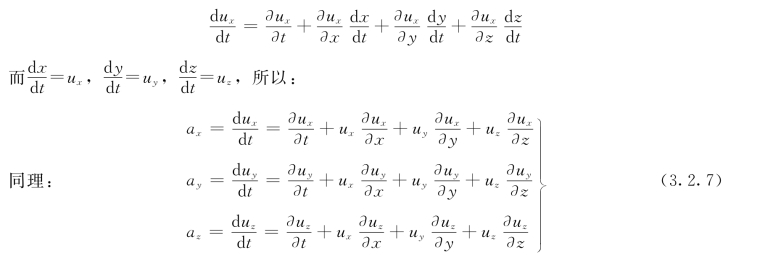
将速度用向量表示为：

而微分算子

u与▽作点乘积，得：

于是加速度的向量表达式为：

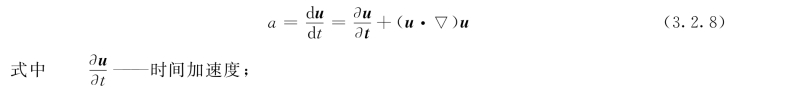
（u·▽）u——位移加速度。

这样，在欧拉法中，流场中任意一点的全加速度是由时间加速度和位移加速度两项组成。

在欧拉法中，运动的几何特征是流线。设在图3.2.1所示的流场中点P处的速度向量为：

通过点P流线的微元弧向量为：

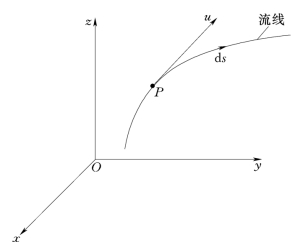
图3.2.1

由于速度u的方向与微元弧向量d s相切，即方向相同，因此，它们的方向系数应该成比例，故得流线的微分方程为：

注意：迹线微分方程（3.2.4）中的t是自变量，而在流线微分方程式 （3.2.9）中的t是参变量，即在积分的过程中是作为常数看待的。

例3.2.1 已知平面不可压缩流体的速度分量为：(www.daowen.com)

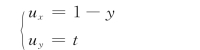
试求：（1）t=0时过（0，0）点的迹线方程。

（2）t=1时过（0，0）点的流线方程。

解：

（1）迹线方程

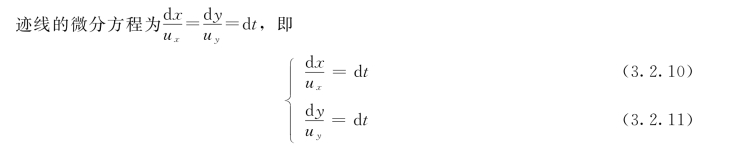
由式（3.2.11）得：

积分得：

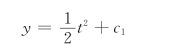
已知t=0时，y=0，得c1=0，所以：

由式（3.2.10）得：

将式（3.2.12）代入得：

积分得：

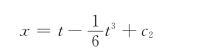
已知t=0时，x=0，得c2=0，则

化简后得：

（2）流线方程

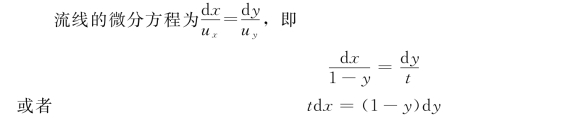
将t作为参数积分得：

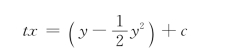
已知t=1时，x=y=0，得c=0，所以：

式 （3.2.14）即为所求流线方程，由于流线的坐标与时间t有关，因此是非恒定流。