如图2.8.2所示，盛有液体的容器绕铅垂轴以等角速度作旋转运动，形成图示状况的相对平衡。此时液体受重力与离心惯性力的作用。取坐标系如图2.8.2所示。单位质量的质量力在三个轴方向的分量可表示如下：

将式（2.8.5）代入液体平衡全微分方程式（2.2.3）得：

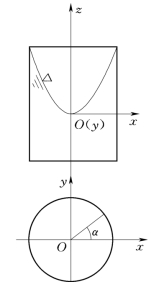
图2.8.2

对上式积分得：

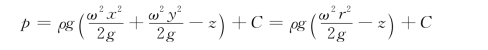
其中：

积分常数C可用下列条件确定。在x=0，y=0，z=0处p=p0，故C=p0代入上式得：

由式（2.8.6）可见，在同一铅垂面上，压强沿水深呈线性分布。当p=pc，pc为常数时，可得匀速圆周运动等压面方程式为：

当pc=p0=pa时，可得自由表面方程为：

由式（2.8.7）、式 （2.8.8）可见，等压面与自由表面均为旋转抛物面。

例2.8.1 一洒水车匀加速在水平道路上行驶，行驶中测得车厢后缘A点的压强为pA=17.64k N/m2，求此时车内水面的斜率与加速度a的大小。已知车长3.0m、宽1.5m、高2.0m，车未开动时车内水深为1.2m，车厢为开敞式。

解：

由题意知液面为大气压强。将p A=17.64k N/m2代入下式：

求得：

(www.daowen.com)

设坐标系统如图2.8.3所示。由几何关系得：

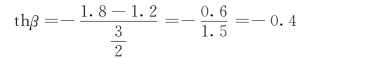
又由式（2.2.8），注意到θ=0°，则

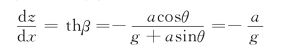
由此解得：

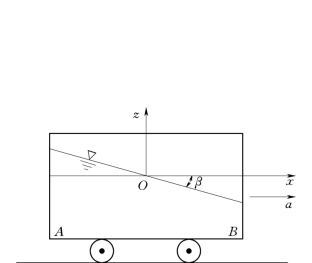
图2.8.3

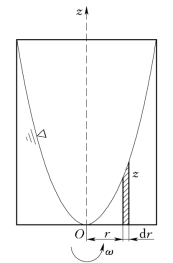
图2.8.4

例2.8.2 如图2.8.4所示的圆柱形容器，其半径为0.15m，当旋转角速度ω=21rad/s时，液面中心恰好触底，试求：

（1）若使容器中水旋转时不会溢出，容器高度需要多少？

（2）容器停止旋转后，容器中的水深为多少？

解：

建立如图2.8.4所示的坐标系。由公式

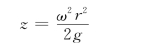
可得：

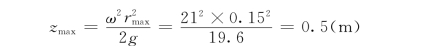
欲求容器内水深的问题，即是求旋转抛物体V 的体积问题。由解析几何可知：

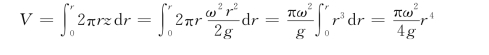
故水深为：