只有部分体积浸没在液体中的物体称为浮体。浮体的平衡条件与潜体相同，但其平衡的稳定条件是不一样的。对于浮体而言，如果重心低于浮心，此时平衡是稳定的，但当重心高于浮心，浮体的平衡仍有稳定的可能。这是因为浮体倾斜之后，浸没在液体内的那部分体积形状有所改变，从而浮心从原来的D点移到D′点，如图2.7.3 （a）所示，但它的重心位置C则不因为倾斜而改变 （如浮体内有液体且有自由液面例外）。这样，浮力Pz和重力G 在一定条件下有可能形成恢复浮体原有平衡状态的力矩。为了进一步阐明这一问题，引入下述概念。

（1）浮面。浮体正浮时液面与浮体表面的交线所围成的平面称为浮面。

（2）浮轴。浮体处于平衡状态时，重心C与浮心D 的连线称为浮轴。

（3）定倾中心。浮体倾斜时，浮轴与浮力作用线的交点M 称为定倾中心。

（4）定倾半径。定倾中心M 与浮心D 间的距离称为定倾半径，记为ρ。

（5）偏心距。重心C与浮心D 间的距离称为偏心距，记为e。

（6）定倾高度。定倾中心M 与重心C间的距离称为定倾高度，记为hm，hm=ρ-e。

浮体倾斜后能否恢复其原平衡位置，取决于重心C和定倾中心M 的相对位置。若浮体倾斜后，ρ＞e，重力G与倾斜后的浮力P′z构成一个使浮体恢复到原来平衡位置的力矩，那么浮体处于稳定平衡状态。反之，若ρ＜e，重力G与倾斜后的浮力P′z构成的力矩将使浮体继续倾倒，浮体处于不稳定平衡状态。当浮体倾斜后，定倾中心M 点与重心C 点重合，即ρ=e，重力G与浮力Pz不会产生力矩，浮体处于随遇平衡。判断浮体在重心高于浮心情况下的平衡稳定性，可归纳为：

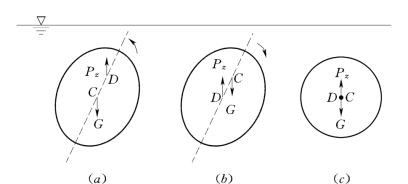
图2.7.2

由式（2.7.2）可见，重心、浮心和定倾中心的位置对浮体平衡的稳定性至关重要。下面推导定倾半径ρ的计算公式。

1.浮体内没有自由表面的液体时

如图2.7.3所示，设浮体倾斜微小角度θ后，浮心由D移至D′，其水平距离为l，则

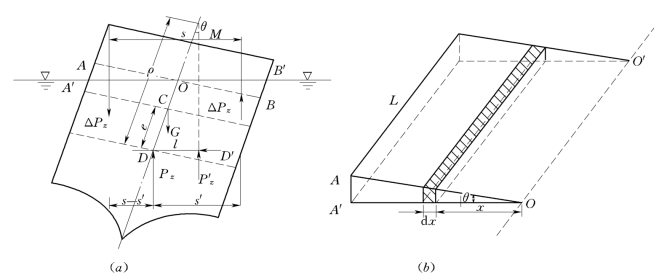
图2.7.3

为求得ρ首先要确定l的大小。浮体倾斜之后，重心的位置没变，浮力的大小亦不变，只是由于排水体积形状变化，浮心位置发生了改变。倾斜后的浮力P′z可以看成是原浮力Pz加上三棱体BOB′引起的浮力ΔPz再减去三棱体AOA′引起的浮力ΔPz。由于浮体的对称性，浸入水中的BOB′和浮出水面的AOA′体积相等，即

根据合力对某轴的力矩等于各分力对该轴的力矩和的原理，对原浮心D取力矩，得：

故求得l为：

下面的问题便是求出ΔPzs。

在三棱体中取出一微小体积d V，如图2.7.3 （b）所示，由于倾斜角θ很小，则tanθ≈θ。故微小体积上的浮力为：

式中 d x——微小体积的底宽；

L——长度；

x——距O点距离。

d Pz对O O 取矩得：

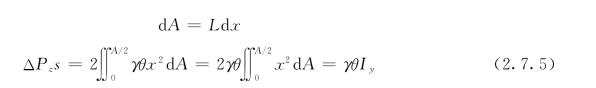
式中 Iy——全部浮面对中心纵轴O—O的惯性矩。

将式（2.7.5）代入式（2.7.4）且注意到P′z=γV，得：

将式（2.7.6）代入式（2.7.3）并注意到sinθ≈θ，得：

式中 V——浮体排开液体的体积。

2.浮体内有自由液面的液体时

浮运有压舱水的沉箱、运输油的船只等都会遇到浮体内有自由液面液体的情形。为保证沉箱浮运及船舶航运的安全，必须考虑其稳定性。

(www.daowen.com)

图2.7.4

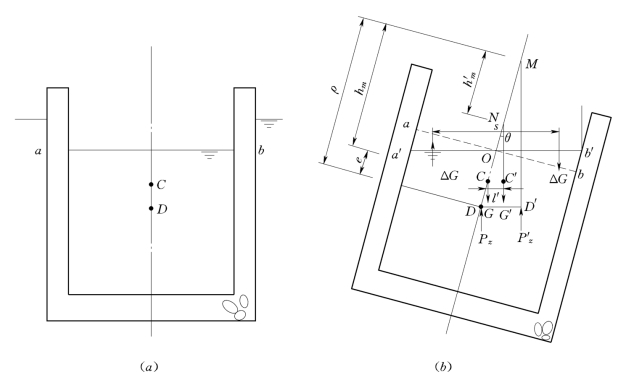
如图2.7.4所示，设一具有压舱水的沉箱遇风浪倾斜时，舱内液面由正浮时的ab变为a′b′ （液面始终保持水平），这时不但浮心由原来的D变为D′，而且重心也由原来的C变为C′。设倾斜后重力作用线交浮轴于N 点，这样定倾高度由原来没有压舱水时的hm变为有压舱水时的h′m，减小了CN 值，即

式中 h′m——有效定倾高度。可用来判断有自由表面液体时浮体的稳定性。

下面推求CN 值的大小。设沉箱浮轴顺时针转动一微小角度θ，箱中自由液面由正浮时的ab变为a′b′，箱内液体在浮轴左侧减少了三棱柱体aOa′相应的水重ΔG，右侧则增加了体积相同的三棱柱体bOb′相应的水重，故倾后浮体重量G′不变，即G′=G。根据合力对某一轴的力矩等于各分力对同一轴力矩的和，对原来重心C点取力矩，得：

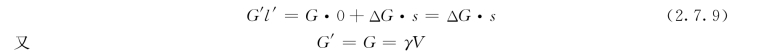
式中 V——沉箱排水体积；

γ——沉箱外面水的容重。

于是

由于倾斜角度θ微小，因此sinθ≈θ，由此：

将式（2.7.11）代入式（2.7.10）得：

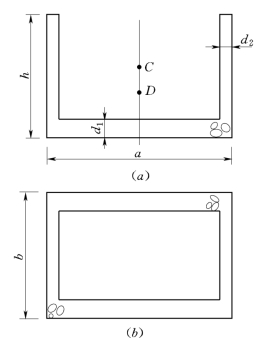
图2.7.5

采用与不带自由表面时求ΔPzs相同的方法可求出：

将式（2.7.13）代入式（2.7.12），得：

式中 γ′——沉箱内液体的容重；

I′y——沉箱内水面对该水面中心纵轴的惯性矩。

当沉箱分舱时，则

由式（2.7.8）计算h′m，当h′m＞0，则沉箱的平衡是稳定的。

例2.7.1 一长a=8m、宽b=6m、高h=5m的钢筋混凝土沉箱，底厚d1=0.5m，侧壁厚d2=0.3m，如图2.7.5所示。海水容重γ=10k N/m3，钢筋混凝土容重γ′=24k N/m3，试检查沉箱内无水时的稳定性。

解：

确定浮体的稳定性问题实际上就是求三心的问题，即求重心、浮心及倾斜后的定倾中心问题。沉箱的重心为：

设沉箱的吃水深度为yD，由于浮体是平衡的，则：

从而得到浮心高度为：

因此

吃水深度为：

定倾半径ρ为：

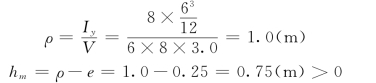
故沉箱的平衡是稳定的。