水利工程中经常遇到受压面为曲面的情况,如弧形闸门、拱坝坝面、弧形闸墩等,这些曲面多数是二向曲面(母线互相平行的柱面),本节讨论的是实际工程中应用较广的二向曲面所受静水总压力的计算。
由于作用在曲面各微小面积上的压力方向是变化的,为了求出全部曲面上的总压力,可将此压力分解为铅直分力和水平分力,如图2.6.1所示。曲面A可看作由无数微小面积d A所组成,而作用在d A上的压力d P可分解为水平分力d Px与铅直分力d Pz。因此:
![]()
作用在整个曲面上压力的水平分力Px为:
![]()
又
![]()
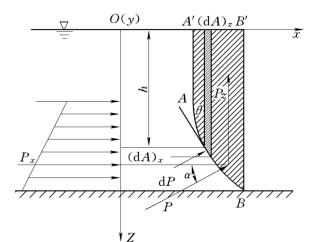
图2.6.1
所以
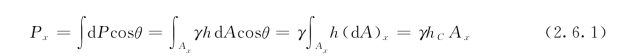
式中 Ax——曲面在铅直面yOz上的投影面积;
hC——投影面Ax的形心在水面下的深度。
由式(2.6.1)可见,作用在曲面上的静水总压力的水平分力Px等于作用于该曲面的铅直投影面上的静水总压力。
作用在曲面AB上的静水总压力的铅直分力Pz:
![]()
从图2.6.1中可以看出:h(d A)z是微小曲面d A 和它在自由水面延长面上的投影(d A)z之间的液柱体积。而∫Azh(d A)z就是整个曲面AB 与其在自由水面延长面上投影Az之间的铅垂柱体ABB′A′的液体体积。柱体ABB′A′称为压力体。压力体的体积Vp用表示。故
![]()
式 (2.6.2)说明,作用在曲面上的静水总压力P的铅直分力Pz等于其压力体内的液体重,而Pz作用线必然通过压力体的重心。
作用于曲面上的静水总压力P的大小与方向可由下式求出:

式中 α——总压力作用线与水平线间的夹角。
P的作用线必通过Px与Pz的交点,但这个交点不一定在曲面上。
值得注意的是Pz的方向,压力体是由受压曲面本身以及它在水面或水面延长面的投影和曲面周界向水面所作的铅直面所围成。当压力体与液体位于曲面的同侧时,铅直压力Pz方向朝下,此时压力体为实压力体;当压力体与液体分别在曲面的两侧时,铅直压力Pz朝上,此时压力体为虚压力体,如图2.6.2所示。其实也可以根据作用在曲面上静水压力的方向来判断其铅直分力的方向。当曲面是凸凹相间的复杂柱面时,可以将曲面分段向液面投影,分别求出铅直压力后再取其代数和。
例2.6.1 用一圆筒闸门挡水 (图2.6.3),圆筒与墙面之间光滑接触。圆筒长度为2m。试求:
(1)圆筒的重量。(www.daowen.com)
(2)圆筒作用于墙上的力。
解:
(1)圆筒的重量
由于圆筒处于平衡状态,所以,圆筒的重量必与水作用于圆筒的铅直分力相等。作用于AB面上的铅直力为:
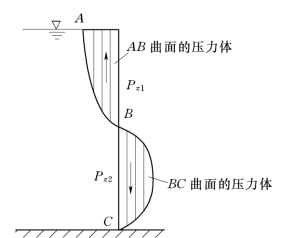
图2.6.2
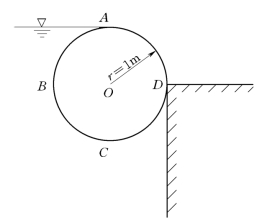
图2.6.3
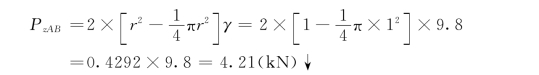
作用于BCD面上的铅直力为:
![]()
因此,圆筒重为W=69.99-4.21=65.78(k N)
(2)圆筒作用于墙上的力
作用于CD与BC面上的水平分力相互抵消。因此,圆筒作用于墙上的水平分力为:
![]()
例2.6.2 一内径为10cm的钢管,壁厚4mm。若管壁许可的张应力 [σ]为1.5×105k N/m2,其管中最大许可压强为多少?
解:
由管道输送液体,圆管壁在内压力作用下承受着张力。假定纵向不产生应力,则管壁承受的张力如图2.6.4所示。现考虑1cm长的圆管段。取此环的一半为隔离体,假定受力为轴对称,管壁承受均布张力T,水对单位长度圆环的压力等于轴中心处压强p与环的直径的乘积,即
![]()
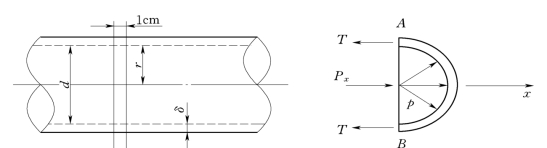
图2.6.4
由力的平衡关系,有
![]()
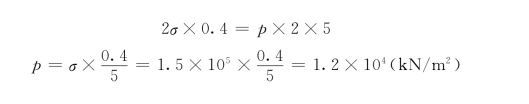
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







