对于任意形状平面，因形状复杂，不能简单地用压强分布图求合力，需要用解析法来确定静水总压力的大小和作用点。

设一平面AB承受水压力，如图2.5.2所示，在坐标平面x Oy内，平面AB与水平面的夹角为θ，其面积为A，右侧承受水的作用，左侧有大气压力作用，水面上也作用着大气压，故只需计算相对压强引起的总压力。图中x Oy平面与水平面的交线为Ox。

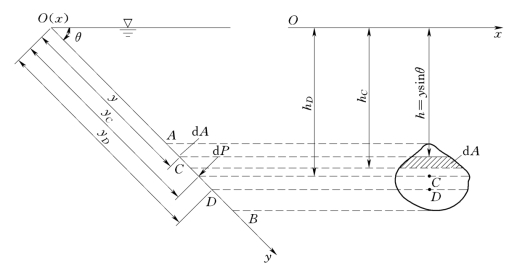
图2.5.2

在AB平面内取任一微小面积d A，其中心点在水面以下的深度为h。作用在d A上的压力为：

其作用方向与d A的内法线方向一致。

作用在全部受压面A上的总压力大小为：

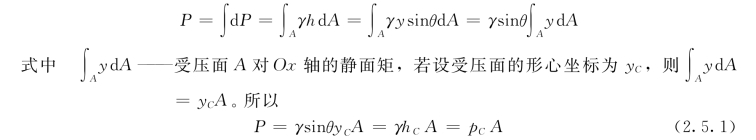
式中 hC——受压面形心在水面下的深度；

pC——受压面形心处的相对压强。

总压力P的作用点D 的位置可应用理论力学中 “合力对任一轴的力矩等于各分力对该轴力矩的代数和”求出。对Ox轴取力矩：

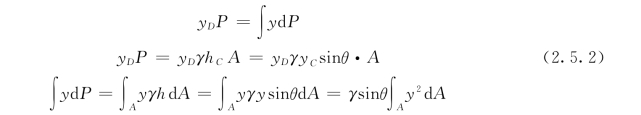
根据平行移轴定理：

式中 Ix——绕Ox轴的惯性矩；

IC——绕形心轴的惯性矩。

所以

比较式（2.5.2）与式（2.5.3）得：

由此可见：

当受压面水平时，yD=yC。一般来说作用点D在形心点C之下。

常见图形的面积A、形心坐标yC以及惯性矩IC列于表2.5.2。

表2.5.2(www.daowen.com)

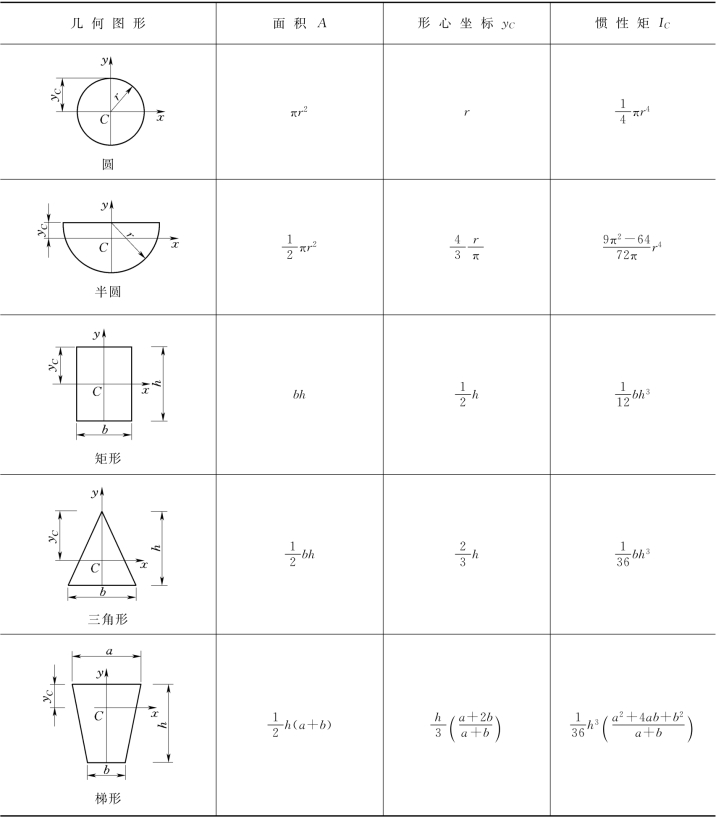
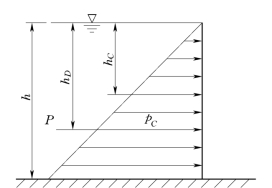
图2.5.3

例2.5.1 在一城市给水系统输水渠道中，有一平板矩形闸门，如图2.5.3所示。闸门宽度b=0.8m，闸门前水深h=1.5m，试求作用在闸门上的静水总压力及其作用点。

解：

例2.5.2 求如图2.5.4所示闸门逆时针打开时z的最小值。闸门为圆形，直径D=1m （压力计的读数为2.94N/cm2）。

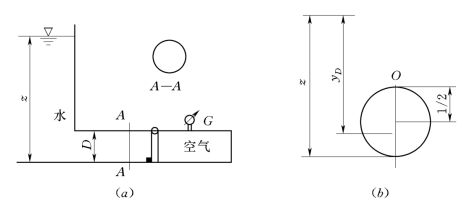
图2.5.4

解：

闸门经受的水压力为：

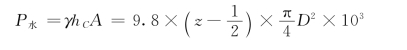
闸门所受的气压为：

静水压力作用点距水面的距离yD为：

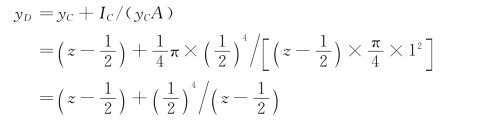
作用点到O的距离：

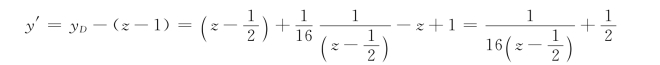
力对O取矩：

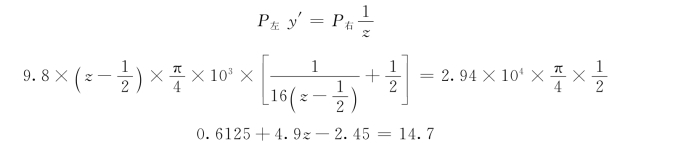
所以