取坐标系如图2.3.1所示，令x Oy平面与容器底面重合，设液面上压强为p0，在质量力只有重力时，作用在单位质量液体上的质量力在各坐标轴上的分量为：

式中 M——液体的质量。

将上式代入式（2.2.3）得：

当液体的密度为常数时，积分后得：

式（2.3.1）就是重力作用下的水静力学基本方程。式中C为积分常数，可由边界条件确定。

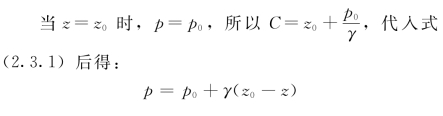
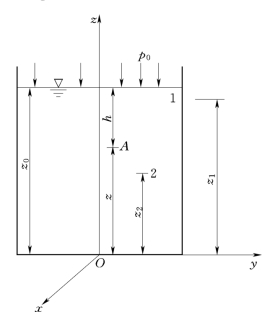
图2.3.1

由图2.3.1可见，z0-z=h，于是静止液体中任一点的压强为：

(www.daowen.com)

式中 h——该点的水深。式 （2.3.2）为水静力学基本方程的另一种形式。

由式（2.3.1），对液体中任意两点有：

由式（2.3.2）、式 （2.3.3）可得出以下结论。在均匀的连续介质中，有：

（1）表面压强p0对液体内部任何点的压强都有影响，也即p0向液体内部的任何地方传递，这就是著名的帕斯卡（B.Pascal）定律。

（2）静水压强与水深成正比，并沿水深按直线规律分布。

（3）当z1=z2时，则p1=p2，即在均质连续的静止液体中，水平面是等压面。

（4）当z1＞z2时，则p1＜p2，即位置较低点的压强大于位置较高点的压强。

如图2.3.2（a）中，M—M 为等压面，N—N 则不是等压面（因非均质），图2.3.2（b）中，1—1也不是等压面（因非连续介质）。

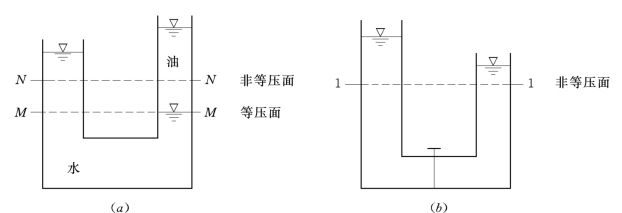
图2.3.2