静水压强有以下两个重要的特性。

1.静水压强的方向沿受作用面的内法线方向

在静止液体中取一块水体，以任一平面N N 将水体切割成Ⅰ和Ⅱ两部分，在切割面上任取一点A，如图2.1.1所示。假设其所受的静水压强p是任意方向的，则p可以被分解为法向分量pn和切向分量τ。而切向分量τ将使液层产生相对运动，这和静止液体的前提相矛盾；若静水压强指向外法线方向，这势必使液体受到拉力作用，而液体是不能承受拉力的。所以，只有受作用面的内法线方向才是静水压强唯一可能的作用方向。

2.静止液体中任一点上各方向压强的大小都相等

在静止液体中任取一点A （x，y，z），并设直角坐标系如图2.1.2所示。在A点附近，取微小四面体ABCD。为方便起见，三个正交面与坐标平面方向一致，棱长分别为d x、d y、d z。设斜面BCD 的面积为d A，其外法线n的方向余弦分别为cos （n，x），cos（n，y），cos（n，z），则

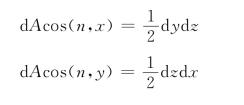
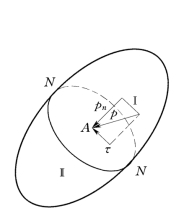
图2.1.1

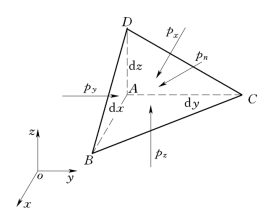
图2.1.2

以px、py、pz和pn分别表示与坐标轴一致的平面和斜面上的平均压强，以Px、Py、Pz、Pn分别表示各面上的总压力（图2.1.2），则有：

(www.daowen.com)

由力的平衡可知，作用于平衡体上的所有外力沿任一坐标轴方向投影的总和等于零，故对x、y、z轴可写出下列平衡方程式：

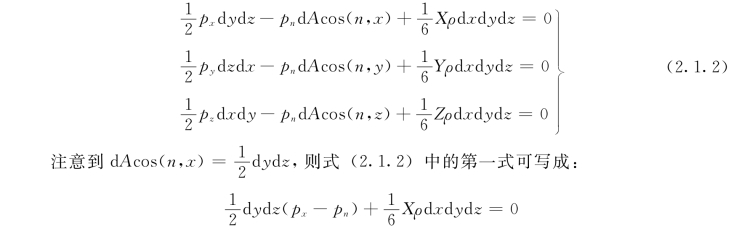
即

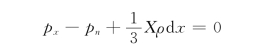
忽略含d x的微小量项，则上式可写为：

同理，由式（2.1.2）中第二、第三式分别可得：

故

式 （2.1.3）表明，静止液体中同一点上的压强大小与作用面的方位无关，即同一点上各个方向静水压强的大小是相等的。但不同点的静水压强则不一定相等，故静水压强是位置坐标的函数，即