液体具有流动性,流动着的液体各流层间可产生内摩擦力以抵抗剪切变形,使各层流动速度不同,这种特性就是黏性。
现在考察如图1.3.1所示的一平面固体边壁处液体的流动。由实验发现,在固体壁面上液体流动的速度为零,随着离开固体壁面距离的增加,速度也增大。取x轴正向沿流动方向,取y轴垂直于x轴。考虑流动中相距为d y的两个液体层,下层的流动速度为u,上层的流动速度为u+d u。由于上下两层间存在着速度差,因此开始在同一条铅垂线上的两个液体质点1、2经过d t时间后移动的距离分别为d1=u d t,d2= (u+d u)d t。由图1.3.1中可知,液体微团产生的角变形为:
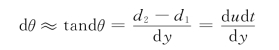
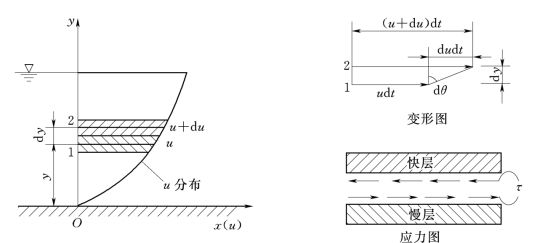
图1.3.1
单位时间产生的角变形称为剪切变形速度,记为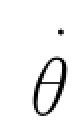 ,则
,则
![]()
由此可见,上述液流中的剪切变形速度等于速度梯度。又由于变形是与应力相关的,所以液层间存在着与剪切变形相应的剪切应力,这是由于运动快的上层带动运动慢的下层向前运动,运动慢的下层阻滞运动快的上层运动所引起的。
牛顿(I.Newton)首先提出计算相邻液层间切应力τ的公式为:
![]()
式 (1.3.7)也称为牛顿内摩擦定律。
作用在相邻液层接触面积A上的总切应力T 为:
![]()
式中 μ——液体的动力黏度,简称黏度,其大小与液体的种类和温度有关,其单位为Pa·s,Pa是压强单位帕斯卡 (简称帕)的单位符号,1Pa=1N/m2;对于20℃的水,μ=1.002×10-3Pa·s。
在水力学中,还常用运动黏度ν来表示液体的黏性,定义为:
![]()
ν的单位为m2/s。
水的运动黏度ν可以按下式计算:
![]()
式中 t——摄氏温度,单位符号为℃。
温度对于流体的黏性有较大的影响。液体的黏性随温度的增加而减小,而气体的黏性则随温度的增加而增加。这是因为液体的黏性力取决于分子间的内聚力,当温度升高时液体分子间的内聚力减小,因此液体的黏性随温度的增加而减小。但是,气体分子的间距很大,内聚力极小,而分子运动非常剧烈,气体的黏性力主要来自分子间的动量交换。当气体的温度升高时,分子运动加剧,分子间的动量交换加大,所以黏性增大。图1.3.2给出了水和空气的运动黏度与温度之间的关系曲线。
在水力学中,将不考虑黏性作用的液体称为理想液体,否则称为实际液体。图1.3.3中的水平线OE表示理想液体。(www.daowen.com)
符合牛顿内摩擦定律,即τ与d u/d y成正比且温度不变时,μ为常数的液体称为牛顿液体,如水、酒精、汽油及水银等。这时切应力与速度梯度之间呈线性关系,如图中OA 线所示。非牛顿液体有下面三种:
(1)理想宾汉液体,如泥浆、油漆、牙膏等。切应力与速度梯度之间的关系如图1.3.3中O′B 线所示,这种液体只有当切应力达到初始屈服应力τy以后才产生变形,之后τ∝d u/d y,μ为常数。
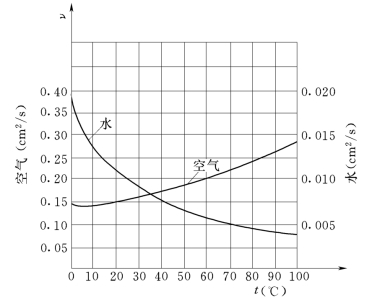
图1.3.2
(2)拟塑性液体,如黏土和石灰的悬浊液、血液及高分子化合物溶液等。随d u/d y的增加μ值减小,如图1.3.3中OC线所示。
(3)膨胀性液体,如淀粉糨糊及浓糖溶液等。随d u/d y的增加,μ值亦增加,如图1.3.3中OD线所示。
水力学中只研究理想液体和牛顿液体。非牛顿液体在化学工程、生物工程中较常遇到。
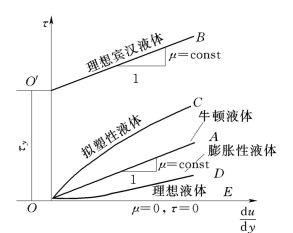
图1.3.3
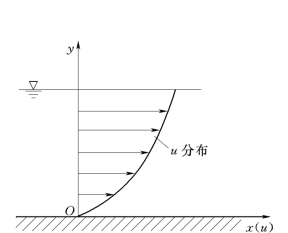
图1.3.4
例1.3.1 液体在平板上流动,如图1.3.4所示,速度u与距平板的垂直距离y的关系为u=2y 2/3。假设液体的动力黏度μ=1.14×10-3Pa·s,试求:距平板1cm和10cm处的速度梯度(d u/d y)及切应力τ。
解:
由u=2y 2/3,得:
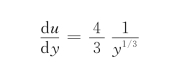
代入已知数据y1=0.01m,y2=0.1m,得:
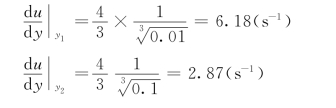
由牛顿内摩擦定律:
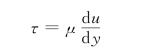
所以
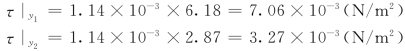
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






