进退法是一种缩小极值区间的算法，算出的结果是一个包含极值的区间，适合在未知极值范围的情况下使用。

其理论依据是f（x）为单谷函数（只有一个极值点），且[a，b]为其极小值点的一个搜索区间。对于任意x1，x2∈[a，b]，如果f（x1）<f（x2），则[a，x2]为极小值的搜索区间，如果f（x1）>f（x2），则[x1，b]为极小值的搜索区间。

因此，在给定初始点x0及初始搜索步长h的情况下，首先以初始步长向前搜索一步，计算f（x0＋h）。

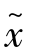如果f（x0）>f（x0＋h），则可知搜索区间为，其中待求。为确定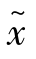，前进一步计算f（x0＋λh），λ为放大系数，且λ>1，直到找到合适的λ∗，使得f（x0＋h）<f（x0＋λ∗h），从而确定搜索区间为[x0，x0＋λ∗h]。

如果f（x0）<f（x0＋h），则可知搜索区间为，其中待求。为确定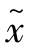，后退一步计算f（x0－λh），λ为缩小系数，且0<λ<1，直到找到合适的λ∗，使得f（x0－λ∗h）>f（x0），从而确定搜索区间为[x0－λ∗h，x0＋h]。

进退法的基本算法步骤如下：

①给定初始点x（0），初始步长h0，令h＝h0，x（1）＝x（0），k＝0；

②令x（4）＝x（1）＋h，k＝k＋1；

③若f（x（4））<f（x（1）），则转到步骤④，否则，转到步骤⑤；

④令x（2）＝x（1），x（1）＝x（4），f（x（2））＝f（x（1）），f（x（1））＝f（x（4）），令h＝2h，转到步骤②；

⑤若k＝1，则转到步骤⑥，否则，转到步骤⑦；

⑥令h＝－h，x（2）＝x（4），f（x（2））＝f（x（4）），转到步骤②；

⑦令x（3）＝x（2），x（2）＝x（1），x（1）＝x（4），停止计算，极小值点包含于区间[x（1），x（3）]或[x（3），x（1）]。

根据以上分析，编写用进退法求解一维函数的极值区间的MATLAB函数fun_JT如下：

其调用格式为

其中，f为目标函数；(www.daowen.com)

x0为初始点；

h0为初始步长；

eps为精度；

minx为目标函数取包含极值的区间左端点；

maxx为目标函数取包含极值的区间右端点。

例5.4　取初始点为0，步长为0.05，用进退法求函数f t（　）＝t4－2t2－t＋1的极值区间。

解：在MATLAB命令窗口中输入：

运行后结果如下：

所以，函数f（t）＝t4－2t2－t＋1的极值区间为[0.350 0，1.550 0]。

例5.5　用进退法求函数f（x）＝x2－10x－36的极值。其中a＝0.1，h＝0.1，e＝0.05。

解：首先编写函数代码如下：

再根据进退法原理编写如下代码：

运行并分别输入参数值，得到如下结果：

即函数极值为－59.109 4。