［题］用一块矩形的铝片做一个截面为等腰梯形的槽。可以做成如图15所示的各种不同的样子。请问应该怎样折叠，折成的角度多大时，金属槽的截面积是最大的？

图14　矩形的铝片

［解］设铁片的宽为l，侧面的宽为x，底面的宽为y。除此之外，我们还要引入一个未知数z，它表示的部分如图17所示。

根据题意，槽的截面积可以表示为：

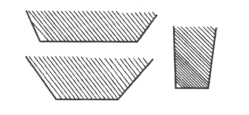
图15　三种等腰梯形的截面

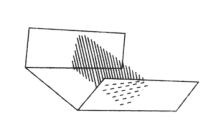
图16　金属槽截面

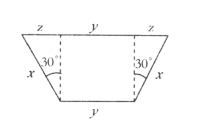
图17　金属槽截面示意图

因此，这个题目就转化为当x、y.z分别为多少时，S的值可以达到最大。(www.daowen.com)

变换上面的等式，得：

S2=（y+z）2（x+z）（x-z）

当S2的值达到最大时，显而易见，3S2的值也将达到最大。3S2可以表示为：

（y+z）（y+z）（x+z）（3x-3z）

这四个乘数的和

y+z+y+z+x+z+3x-3z=4x+2y=2l

2l是一个定值。由前文的结论可知，在这种情况下，只有当y+z=z+x=3x-3z时，3S2的值才能达到最大。

由上面的等式以及2x+y=l，可以得出

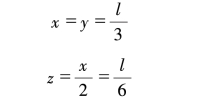
此外，由图17我们可知，z的长度是x长度的一半，所以，z对着的角是30°。因此，槽的底面和斜面间的夹角等于

90°+30°=120°

由此可知，当这个槽的侧面各边折成正六边形的三个相邻边时，它的截面达到最大面积。