波格丹诺夫·别尔斯基有一幅名画——《口算》，但大家往往忽略了里面的题目。你能够很快根据图中的题目得出答案吗？

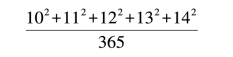
图8　名画中的难题

这道题目看上去并不是那么容易，但还是有学生很快就算出来了，因为学生掌握了数字的特性。10、11、12、13、14这几个数其实具有一种十分有趣的特性，那就是：

102+112+122=132+142

因为102+112+122=132+142=100+121+144=365，所以很容易得出图中题目的答案为2。

我们接下来探讨一下，是否还有这样的5个连续整数组成的数列，也和10、11、12、13、14这个数列一样，前3个数字的平方和等于后2个数字的平方和。

［解］设x为所求数列的第一个数，按要求可列出方程：

x2+（x+1）2+（x+2）2=（x+3）2+（x+4）2

为了简便一些，我们可以设所求数列的第二个数字为x：

（x-1）2+x2+（x+1）2=（x+2）2+（x+3）2(www.daowen.com)

简化可得：

x2-10x-11=0

解方程得：

即x1=11，x2=-1

因此，具有这种特性的数列共有两组，其中一组就是题目中的10、11、12、13、14。

而另一组则是：

-2、-1、0、1、2

事实上，

（-2）2+（-1）2+02=12+22。