土地测量员在地面上画垂线的方法既简单又精确（图6）：

假设测量员需要画一条通过点A而且垂直于MN的直线。第一步：只需从A点出发，沿AM方向取3a，其中a为任意长度；第二步，在一条绳子上打三个结，并且使绳结与绳结之间的距离分别为4a和5a。再将绳子的两端分别固定在A和B的位置，然后把整条绳子拉紧。

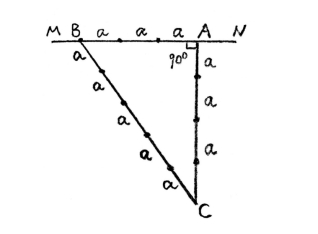
图6　土地测量员画垂线的方法

此时，如图6所示，角A为直角，AC就是所求的垂直于MN的直线。

几千年前古埃及的建筑师在修建金字塔时已使用过这个非常古老的方法。它的原理非常简单。根据勾股定理，任意一个三边比例成3∶4∶5的三角形，都一定是一个直角三角形，因为

32+42=52

不仅仅只有3、4、5，我们知道，还有无数个正整数a、b、c能够满足下面的关系式：

a 2+b2=c2

根据勾股定理，在这些数字中，因为a和b可以作直角三角形的直角边的边长，因此，它们也被叫作“直角边”，或者“勾”和“股”；而c被称为“斜边”或者“弦”。

如果a、b、c是三个整数勾股弦数，那么，当p是一个整数时，pa、pb、pc也会是整数勾股弦数。反过来，假如有这样一组拥有一个共同乘数的整数勾股弦数，那么当我们用这个共同的乘数去除这组勾股弦数后，得到的肯定是一组新的整数勾股弦数。因此，我们可以只讨论最简单的三个勾股弦数。

如果一个直角三角形的两个直角边a和b都是偶数，那么a2+b2也一定会是偶数，那么这个直角三角形的斜边c也是一个偶数。这时，a、b、c就有了公因数2，这样的三角形就不是我们所要求的勾股数。

还有一种情况：两条直角边都是奇数，而斜边是偶数。我们可以证明，设两条直角边分别为2x+1和2y+1。那么，它们的平方和为：

4x2+4x+1+4y2+4y+1=4（x2+x+y2+y）+2

这个数字是一个偶数，它可以被4除余2。很明显，它不是一个偶数的平方，因为所有偶数的平方都可以被4整除。所以，这种假设是不成立的。

我们所要求的直角三角形肯定有一条直角边是偶数，另一个直角边是奇数。因为a2+b2是一个奇数，所以斜边也应该是一个奇数。假定在两条直角边中，a是奇数，b是偶数。由a2+b2=c2得出：

a2=c2-b2=（c+b）（c-b）

（c+b）和（c-b）是互为素数的两个整数。

的确，如果除1之外，这两个数有一个其他的公因数，那么对于这两个数来说，它们的和

（c+b）+（c-b）=2c

它们的差

（c+b）-（c-b）=2b

它们的积

（c+b）（c-b）=a2

就能被一个公因数整除。也就是说，2c、2b、a2有一个公因数。因为a是一个奇数，所以，这个公因数也不是2。也就是说，a、b、c有一个公因数，不符合题目要求。所以，（c+b）和（c-b）互为素数。

如果要互为素数的两个数的乘积是一个数的平方，那么这两个数自己肯定也是一个数的平方：(www.daowen.com)

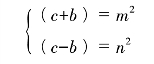
解方程可以得到：

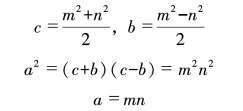
当m和n是一对互为素数的奇数时，我们所讨论的整数勾股数就可以表达为：

反过来，对于任意的奇数m和n，我们都能利用上面的公式给出三个整数勾股弦数。、b、c。

下面就是对于不同的m和n，我们所得出的符合条件的部分整数勾股弦数：

m=3，　n=1　　32+42=52

m=5，　n=1　　5+12=32

m=7，　n=1　　72+242=252

m=9，　n=1　　92+402=412

m=11，　n=1　　　112+602=612

m=13，　n=1　　　132+842=852

m=5，　n=3　　　152+82=172

m=7，　n=3　　212+202=292

m=11，　n=3　　332+562=652

m=13，　n=3　　392+802=892

m=7，　n=5　　352+122=372

m=9，　n=5　　452+282=532

m=11，　n=5　　552+482=732

m=13，　n=5　　652+72=972

m=9，　n=7　　632+162=652

m=11，　n=7　　　772+362=852

勾股数还有许多非常有意思的特性，例如：如果一个直角三角形的一条直角边小于3，另一条直角边小于4，那么，它的斜边应当小于5。

如果你有兴趣的话，可以对此进行证明。