［题］三姐妹带着母鸡到集市上去卖。大姐带了10只鸡，二姐带了16只鸡，三姐带了26只鸡。上午她们按照相同的价格各自卖出了一部分母鸡。到了下午，她们担心卖不完，于是降价销售，又按照相同的价格把各自的母鸡全部卖完了。晚上回家的时候，她们每个人的钱都是一样多的，都是35元。

请问，她们上午卖的什么价格，下午卖的又是什么价格？

［解］设三姐妹上午所卖出的母鸡的只数分别为x、y、z，三姐妹下午所卖出的母鸡的只数分别为10-x、16-y、26-z。设母鸡上午的价格为m，母鸡下午的价格为n。

三姐妹中第一位所得为：

mx+n（10-x）

第二位所得为：

my+n（16-y）

第三位所得为：

mz+n（26-z）

由题目可知，三人卖的钱都是35元，我们可以列出下面这三个方程：

先用方程③减去方程①，再减去方程②。之后，我们可以得到如下方程组：

用上面方程组中的方程①除以方程②，可得：

因为x、y、z都是整数，所以x-z，y-z也都是整数。要使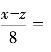成立，x-z必须能被8整除，y-z必须能被5整除。(www.daowen.com)

设，

那么，

因为x＞z，t不但是一个整数，而且必须是一个正数。

又因为

x＜10，那么

z+8t＜10

只有一组数能够使不等式成立，那就是z=1，t=1。把z和t的值代入方程

可以得出：x=9，y=6。

将x、y、z的值代入下面方程组：

可以求得：

所以，上午时，母鸡每只3.75元；下午时，母鸡每只1.25元。