［题］你在商店里买了一件19块钱的东西，但是你所有的钞票都是2块的，而老板所有的钞票都是5块的，那么你怎样付给老板钱？

其实这个问题可以换一种说法：你应该给老板几张2块钱的钞票，而老板应该找给你几张5元的钞票，而这两者的差额刚好是19块钱。

我们可以设两个未知数x、y，其中x表示你给商店的2元钞票的张数，y表示商店找给你的5元钞票的张数。

可以列出方程：

2x-5y=19

这个方程中有两个未知数，所以它可以有无数组解，但是，在这个题目中，x、y只能都是正整数。要找出这样的解并不是一件容易的事。这就是为什么我们要寻找解这类“不定方程”的方法。欧洲著名数学家刁藩都找到了解答这种方程的方法，因此这类方程也常常被称为“刁藩都方程”。

［解］我们根据题目来讲一讲怎么解这类方程。

2x-5y=19

我们要做的就是在方程中找出同时为正整数的x和y的值。

把2x分离出来：2x=19+5y，经过计算可以得到：

因为x、9、y均为正整数，所以，最后一项也应该是整数。令：

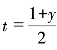2t=1+y，y=2t-1

将y的表达式代入前面x的表达式中，得出：

x=9+2（2t-1）+t=5t+7

现在，让我们来看一下下面两个式子：

只要t是整数，那么x和y的值也一定都是整数。因为x和y不仅是整数，而且还是正数，所以

7+5t＞0

2t-1＞0

解这两个不等式：

所以，t的数值要大于。它可能的取值有以下几种情况：

t=1，2，3，4，……(www.daowen.com)

相应的，x和y可能的取值就是：

x=7+5t=12，17，22，27，……

y=2t-1=1，3，5，7，……

现在我们知道了，你可以付给商店12张2元的钞票，商店找给你1张5元的钞票：

12×2-5=19，

你也可以给商店17张2元的钞票，同时商店找给你3张5元的钞票：

17×2-3×5=19，

……

理论上，这道题可以有无数种的解，但因为顾客和商店拥有钞票的数都不是无限的，所以这道题的答案在实际中是有限的。比方说，如果双方都只有15张钞票时，那么付款方式就只能有一种：顾客给商店12张2元的钞票，商店给顾客1张5元的钞票。所以说，不定方程虽然理论上有无穷多解，但现实中常常只有有限的几种答案。

回到题目上来，如果顾客只有5元的钞票，而商店只有2元的钞票，那么应该如何付款呢？用上面的方法来解这个问题，我们可以得到一系列解：

x=5，7，9，11，……

y=3，8，13，18，……

通过计算，我们可以验证这些解都是正确的。

这道题目还能这样思考：既然付5元找2元就等于“顾客付给商店几张面值为5元的钞票，而商店找给顾客几张面值为2元的钞票，商店最后收进的钱恰好是19元”，因此，这个题目仍然可以用之前列出的方程来解答：

2x-5y=19

但要求x＜0，y＜0：

所以：

取t=-2，-3，-4，-5……根据上面的公式，我们可以计算出这些x和y的数值：

第一组解x=-3，y=-5表示，顾客“付负3张2元的钞票，而找回负5张5元的钞票”。用生活语言表达就是：顾客付5张5元的钞票，而找回了3张2元的钞票。其他的解也可以用同样方式来进行解释。