［题］有一次，大名鼎鼎的物理学家爱因斯坦生病了，为了逗他开心，他的朋友给他出了道题目（图3）：

图3　分针与时针运动示意图

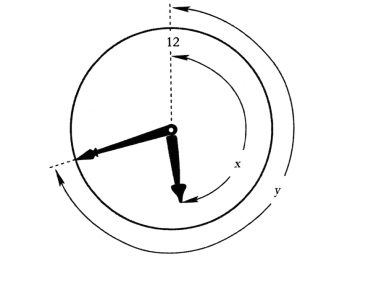
“假设表针的位置是在12点钟。在这个位置上，如果把分针和时针对调一下，它们所指示的时间还是存在的。但是在其他的时间，如果把两针对调之后所出现的结果就有悖常理了。例如在6点钟时，如果我们把两针对调出现的结果是不可能存在的：当时针指向12，分针绝对不会指向6。因此可以引出这个问题：表针在什么位置的时候，分针和时针可以对调，并且所指的时间仍然是可能存在的？”

爱因斯坦想了想，然后回答：“这个问题很有趣，可惜消磨不了多长时间，我想我已经找到问题的正确答案了。”

他从床上坐起来，用笔在纸上画出了有关这个问题的草图，然后很快地解答出来，所花的时间比我叙述这个问题所花的时间还要短。

爱因斯坦是怎样解答这道题的呢？

［解］首先，让我们把表盘圆周分成相等的60份，然后以圆周的为单位，计算表针从12开始所走的距离。

假设我们所求的针的位置在时针从12起走了x个刻度，分针走了y个刻度。时针12个小时能走过60个刻度，也就是说，时针每小时能走5个刻度，那么它走过x个刻度要小时。换句话说，在表走到12点以后，又过了小时。分针走过y个刻度所用时间是y分钟，也就是小时。也就是说，分针是在小时之前经过12的。或者说，两针在12处重合之后又过了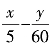小时。这个数是从0到11之间的一个整数，因为它表示12点之后又过去了几个整小时。

当两针的位置调换了之后，我们可以用同样的方法求出从12点到表针所指示的时间经过了个小时。这个数仍然是在0到11之间的整数。

我们可以列出联立方程：

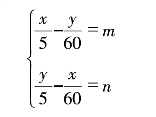
由这个联立方程我们可以解出：(www.daowen.com)

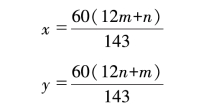
在这个方程中，m和n都可以任取从0到11之间的任意整数。所以，要想确定全部所求表针的位置，只需要把从0到11之间的全部整数都代入到上述的方程中。因为m可以取的12个数中任何一个都可以与n可以取的12个数中的任意一个组合，所以，很多人都会觉得这道题有12×12=144个解。可是事实上只有143个解。因为在m=0，n=0和m=11，n=11时，表针所处的是同一位置。

我们不讨论所有可能出现的位置，只看看两个例子：

第一例：

m=1，n=1，

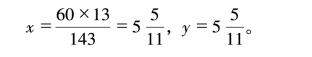
所指的时间就是1点分，此时两针重合；当两针重合时，它们当然可以彼此对调。

第二例：

m=8，n=5，

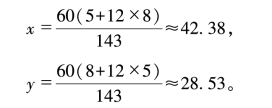
相对应的时间是：8点28.53分和5点42.38分。