我们在生活中做木工活时常常会碰到这样的事情：手头的木料不刚好是自己需要的尺寸，如图77所示。那么我们只好想办法改变木料的尺寸来解决这个问题，这时几何知识就能给我们很多帮助。

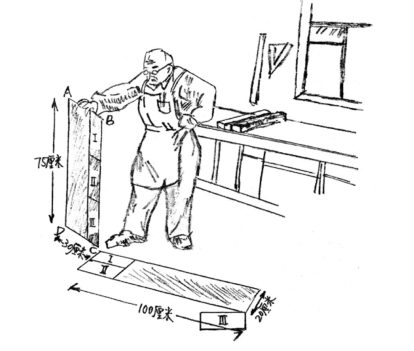
图77　锯三次，拼一次，如何把木板接到足够长？

假设你需要一块长1米宽20厘米的木板，但是你身边并没有这样尺寸的木板，你只有一块75厘米宽30厘米的木板，这块木板比你所需要的木板要短粗一些。我们该怎么办呢？

第一个想法当然就是把这块木板沿着边缘锯掉10厘米的宽度，然后把这根锯下来的木头再锯成长25厘米的三段，并把其中的两段接到大木板上，如图77所示。这样的做法虽能到达目的但是并不简便，操作起来很复杂，至少需要锯三次，拼接二次。你能想到一个办法，只锯三次，拼接一次就能达到目的吗？

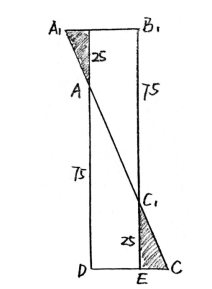
图78　正确的补法

操作图解如图78所示，把木板ABCD沿对角线AC锯开，然后把三角形ABC沿对角线和另外半块三角形ADC移开一段距离C1E，C1E这个长度就等于木板所缺少的长度，也就是25厘米，这两个半块长度加起来就刚好等于1米了。现在把它们在AC1处拼接起来，然后把多余的部分——两个画着阴影部分的小三角形锯掉，就等到我们所需要的木板了。

实际上，两个三角形ADC和C1EC是相似三角形，我们得到：(www.daowen.com)

AD∶DC=C1E∶EC

得到

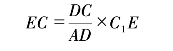
或者

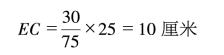
最后

DE=DC-EC=30-10=20厘米