一个工人拿到一个圆锥形的材料，要求是尽量不浪费材料的得到一个圆柱体。那么问题来了，到底是处理成又细又长的圆柱时浪费的材料少，还是处理成又短又粗的圆柱时浪费的材料少呢？换句话说，他思考的是，如何在这个圆锥体中得到体积最大的圆柱体。

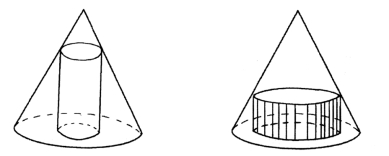
图74—75　哪一种去掉的材料少？

我们可以将这个问题转换为一个几何题目，如图76所示，设ABC代表的是圆锥通过轴线的截面，高BD用h表示，它的底面半径AD=DC，用R表示。假设工人处理出来的圆柱的截面为MNOP，我们需要

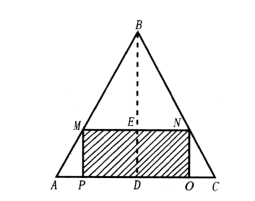
图76　圆锥和圆柱通过轴线的截面

求出圆柱的上表面和圆锥顶点B的距离BE，我们用x来表示：

ME∶AD=BE∶BD

就是

r∶R=x∶h

由这个式子可以得到圆柱的底面半径r（PD或ME）：

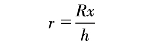
因为圆柱的高ED等于h-x，所以它的体积等于：(www.daowen.com)

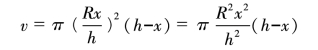
这样就得到：

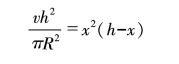
在中，h、π和R都是定值，只有v是变化的。那么，我们要做的就是找到一个x的值，使v的值最大。

我们发现，v会随着，也就是随着x2（h-x）而变化，它们达到最大值时是同步的。那么，x2（h-x）什么时候才能达到最大值呢？这个式子中有三个变量：x，x，（h-x），如果它们的和是定值，那么它们的乘积将在三个乘数相等时达到最大。我们将等式两边同时乘以2，会得到：

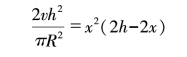
我们将右边三个乘数相加，会发现它们的和是固定的：

x+x+2h-2x=2h

因此，当这三个乘数相等的时候，它们的乘积是最大的，即是：

即当时，将达到最大值。此时圆柱的体积v也达到了最大值。我们利用自己的数学知识计算之后就知道工人应该怎样操作来获得体积最大的圆柱体了。只需要保证圆柱的上表面离圆锥顶的距离为圆柱高的三分之二即可完成任务。